Метод художника для удаления невидимых частей поверхностей, страница 4

if (delta>=0)

delta += b2*( -x*2 + 1 ); //отрицательное приращение

else

{                         //положительное приращение

delta+=a2*(y*2+1)+b2*(-x*2+1);

y++;

}                         //y увеличивается на 1

x--;                              //x уменьшается на 1

}

getch();

closegraph();                     //выход из графического режима

}

Задача № 13.  Задан отрезок с экранными координатами  ((10, 10), (610, 410)). Рассмотреть на примере вывода этого отрезка алгоритм симметричного ЦДА и указать координаты первых пяти точек этого отрезка.

x0=10, y0=10, x1=610, y1=410

dx=x1-x0=600>0, dy=y1-y0=400>0, ex=1, ey=1, resx=512, resy=512

1.  resx=512+600=1112>1024

x=10+1=11, resx=1112-1*1024=88, resy=512+400=912<1024, y=10 (11,10)

2.  resx=88+600=688<1024, x=11

resy=912+400=1312>1024, y=10+1=11, resy=1312-1024=288 (11,11)

3.  resx=688+600=1288>1024, x=11+1=12, resx=1288-1024=264

resy=288+400=688<1024, y=11 (12,11)

4.  resx=264+600=864<1024, x=12

resy=688+400=1088>1024, y=11+1=12, resy=1088-1024=64 (12,12)

5.  resx=864+600=1464>1024, x=12+1=13, resx=1464-1024=440

resy=64+400=464<1024, y=12 (13,12)

Задача №14. Построчный алгоритм закраски с использованием затравки. Рассмотреть пример.

Разберем, как будет осуществляться закраска этим алгоритмом трапеции, приведенной на рис. 9.

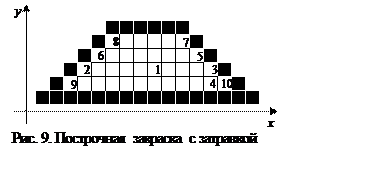
Обозначим 1 заданную затравку. Заносим точку 1 в стек, а затем в цикле извлекаем из стека. Тогда абсцисса точки 2 – это X_лев, а абсцисса точки 3 – это X_прав. После закраски горизонтального отрезка, содержащего точку 1, просматривается нижний отрезок для X_лев ≤ X ≤ X_прави точка 4 заносится в стек. Просматривается верхний отрезок для X_лев ≤ X ≤ X_прави точка 5 заносится в стек. Таким образом, закрашен один горизонтальный отрезок и две точки (сначала точка 4, а потом точка 5) занесены в стек. Так как стек не пуст, то извлекаем точку 5 (она была занесена в стек последней) и закрашиваем горизонтальный отрезок, содержащий эту точку. В этом случае абсцисса точки 6 – это X_лев, а абсцисса точки 5 – это X_прав. Просматриваем нижний отрезок для X_лев ≤ X ≤ X_прав, он весь закрашен. Просматриваем верхний отрезок для X_лев ≤ X ≤ X_прави заносим точку 7 в стек. Закрашены два горизонтальных отрезка, и две точки находятся в стеке – точка 4 и точка 7. Извлекаем точку 7 из стека (она была занесена в стек последней) и закрашиваем горизонтальный отрезок, содержащий эту точку. В этом случае абсцисса точки 8 – это X_лев, а абсцисса точки 7 – это X_прав. Отрезок, расположенный ниже, уже закрашен, а выше расположена граница области. В стеке осталась только одна точка – точка 4. Извлекаем ее из стека и закрашиваем горизонтальный отрезок, содержащий эту точку, от точки 9 (X_лев) до точки 10 (X_прав). Просматриваем нижний отрезок для  X_лев ≤ X ≤ X_прав, но он является границей области. Просматриваем для X_лев ≤ X ≤ X_правверхний отрезок, но он уже закрашен. В стек ничего не заносится. Стек пуст. Область закрашена.

Задача № 15. Разработать программу, реализующую следующее построение. Строится заполненный круг радиуса R, затем четыре заполненных круга радиуса R/2, которые удалены от центра исходного круга на расстояние 2R. Этот процесс применяется к каждому кругу и т. д. Выполнить данное построение с помощью рекурсии, глубина которой определяется условием R≥4.

#include <graphics.h>

#include <math.h>

#include <conio.h>

#include <stdio.h>

//Функцияпостроениязвезды

void krug(float x0,float y0,float r)