Метод художника для удаления невидимых частей поверхностей, страница 5

{

factor=0.0174633;

int i;

float r_half, r_double, phi;

if (r<4) return; //r>=5

moveto(x0+r,y0);  //Переход на начальную точку вывода звезды

//вывод круга

circle(x0,y0,r)

r_half=0.5*r; r_double=2.*r;//Вычисление параметров для рекурсивного вызова

//Цикл вывода окружающих кругов

for(i=0;i<4;i++)            

{

phi=(36+72*i)*factor; 

krug(x0+r_double*cos(phi),y0+r_double*sin(phi),r_half);

}

}

main()

{

//Инициализацияграфическогорежима:

int graphdriver= DETECT, graphmode, n=100;

initgraph(&graphdriver,&graphmode,"C:\\BC\\BGI");

krug(getmaxx()/2,getmaxy()/2,getmaxy()/7);  //Запускпостроения

getch();            //Ожидание нажатия любой клавиши

closegraph ();   //Выход из графического режима

}

Задача № 16. Пусть даны координаты точки S(4, 5, 2), плоскость P, которая задаётся векторами u₁ = (0, 1, 0), u₂ = (0, 0, 1) и r₀ = (1, 1, 1). Найти координаты (x′, y′) параллельной проекции точки S на плоскость P в направлении вектора u = (1, 0.2, 0.3).

r=S, r-r0=(3,4,1)

(U1,U2,U)=1

x’=(r-r0,U2,U)=3.4

y’=(r-r0,U1,U)=-0.1

Задача № 17. Пусть даны координаты точки S(2, 3, 4), плоскость P, которая задаётся векторами u₁ = (0, 1, 0), u₂ = (0, 0, 1) и r₀ = (1, 1, 1). Найти координаты (x′, y′) параллельной проекции точки S на плоскость P в направлении вектора u = (1, 0.5, 0.8).

r-r0=(1,2,3)

(U1,U2,U)=1

x’=(r-r0,U2,U)=1.5

y’=(r-r0,U1,U)=-2.2

Задача № 18. Разработать программу, которая выводит на экран замкнутый многоугольник и заполняет его буквами «С» размером 8x8 пикселов.

char pattern[]=

{

0x1C,            // 00011100

0x22,            // 00100010

0x41,            // 01000001

0x40,            // 01000000

0x40,            // 01000000

0x22,            // 00100010

0x1C,            // 00011100

0x0              // 00000000

};

#include <graphics.h>

#include <conio.h>

#include <stdlib.h>

// Шаблон буквы О

char pattern[]=

{

0x1C,            // 00011100

0x22,            // 00100010

0x41,            // 01000001

0x41,            // 01000001

0x41,            // 01000001

0x22,            // 00100010

0x1C,            // 00011100

0x0              // 00000000

};

// Координаты вершин многоугольника

int poly[]=

{

30, 10,

50, 0,

200, 100,

100, 150,

50, 30,

};

void main()

{

// Инициализация графики

int gdriver=DETECT, gmode;

initgraph(&gdriver, &gmode, "");

// Установка палитры закраски

setfillpattern(pattern, WHITE);

// Вывод закрашенного многоугольника

fillpoly(sizeof(poly)/(sizeof(int)*2), poly);

getch(); // Ожидание нажатия клавиши

closegraph(); // Выход из графического режима

}

Задача №19. Пусть заданы координаты точки (1, 2, 3), единичный вектор 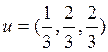 и угол φ=90⁰. Найти координаты (x′, y′, z′) точки после поворота ее на угол φ вокруг вектора u.

UU^T=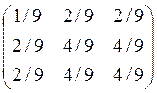

E- UU^T=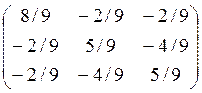

cos φ(E- UU^T)=0* E- UU^T=0

sin φ=1

r'=A*r

A=UU^T+cos φ(E- UU^T)+sin φ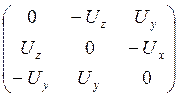

A=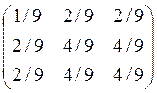+0+1*=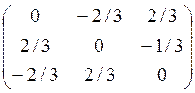

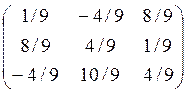
(x′, y′, z′)=*=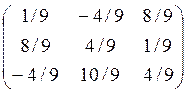

Задача № 20. Пусть задан отрезок с экранными координатами ((0, 0), (5, 3)). Рассмотреть на примере вывода этого отрезка алгоритм простого ЦДА и указать последовательность точек, которые будут сгенерированы этим алгоритмом.

x0=0, y0=0, x1=5, y1=3

|5-0|>|3-0|

l=|x1-x0|=|5-0|=5

dx=(x1-x0)/l=5/5=1, dy=(y1-y0)/l=3/5

ex=1, ey=1

rez=0.5

1.  (0,0)

rez=0.5+3/5=1.1, x=0+1*1=1, y=0+1*1=1, rez=1.1-1=0.1 (1,1)

2.  x=1+1*1=2, rez=0.1+3/5=0.7 (2,1)

3.  x=2+1*1=3, rez=0.7+3/5=1.3, y=1+1*1=2, rez=1.3-1=0.3 (3,2)

4.  x=3+1*1=4, rez=0.3+3/5=0.9 (4,2)

5.  x=4+1*1=5, rez=0.9+3/5=1.5, y=2+1*1=3, rez=1.5-1=0.5 (5,3)