Расчетный тормозной коэффициент

20. Расчетный тормозной коэффициент.

Тормозная сила поезда равна сумме тормозных сил всех тормозных колодок: В = SКj_к. Коэффициент трения зависит от материала тормозной колодки и колеса, состояния поверхностей трения, температуры, нажатия и скорости движения. Расчет коэффициента трения производится по эмпирическим формулам, из которых следует, что с ростом скорости коэффициент трения уменьшается. Это является недостатком колодочного тормоза, так как желательно иметь постоянную тормозную силу во всем диапазоне скоростей.  Для облегчения расчетов для составов с большим количеством вагонов разных типов и чтобы не вводить в расчет зависимость коэффициента трения от силы нажатия на колодку, используют расчетное нажатие на колодку и расчетный коэффициент трения. Для сохранения величины тормозной силы необходимо, чтобы соблюдалось равенство SКj_к = j_крSК_р. Поскольку приведенное равенство должно соблюдаться для любой тормозной колодки в составе поезда, то для определения расчетного тормозного коэффициента необходимо знать действительное нажатие К, действительный коэффициент трения j_к и расчетный коэффициент трения j_кр: . Действительный коэффициент трения можно определить по известным эмпирическим формулам, а величину расчетного коэффициента трения – по тем же формулам, но для среднего значения нажатия при груженом и порожнем режимах торможения.

При использовании расчетного тормозного коэффициента тормозная сила будет равна В = j_крSК_р. Удельная тормозная сила . Таким образом, под расчетным тормозным коэффициентом поезда понимают расчетную силу нажатия тормозных колодок, приходящуюся на 1 кН веса поезда. Минимальная величина расчетного тормозного коэффициента поезда нормируется для различных типов поездов. На практике величина 100u_р используется для определения максимально допустимых скоростей движения по элементам профиля, имеющими различные уклоны. По номограммам, приведенным в справочной литературе возможно решение следующих задач:

- определение тормозного пути по заданной скорости движения и расчетному тормозному коэффициенту;

- определение допустимой скорости движения по элементам профиля при заданном тормозном пути и расчетному тормозному коэффициенту;

- определение требуемого расчетного тормозного коэффициента по заданной скорости движения и тормозному пути;

- определение допустимой величины уклона по заданной скорости движения, тормозному пути и расчетному тормозному коэффициенту.

Для нормальной реализации процесса торможения необходимо, чтобы тормозная сила была не более силы сцепления колес с рельсами. В противном случае происходит заклинивание колеса (так называемый юз). При этом возможно повреждение колесной пары (ползун) с невозможностью продолжать дальнейшее движение. В_кп £ G_кпY_кп, т.е. j_кпК_кп £ G_кпY_кп. Следовательно

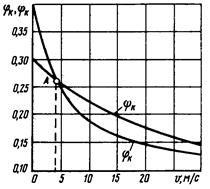
.Отношение наибольшей силы нажатия тормозных колодок к нагрузке на ось колесной пары называют коэффициентом нажатия тормозных колодок: . Для нормальной реализации тормозной силы необходимо, чтобы коэффициент нажатия тормозных колодок был меньше отношения коэффициента сцепления и коэффициента трения. Так как коэффициент сцепления колес с рельсами зависит от скорости в меньшей степени, чем коэффициент трения, то наибольшая опасность заклинивания колесный пар при торможении возникает в зоне малых скоростей. В зоне скоростей V < V_А особенно опасен юз заторможенной колесной пары при трогании поезда. При скорости 5-8 км/ч коэффициент сцепления оказывается в 3-5 раз меньше коэффициента трения колодки и восстановить вращение колеса обычно уже не удается. Для ликвидации юза возможно использование противоюзовой защиты, работа которой основана на резком снижении давления в тормозном цилиндре и затем медленном его нарастании. Важным вопросом любого вида торможения является его устойчивость. При торможении на площадке тормозная сила всегда обеспечивает замедление поезда – т.е. торможение устойчиво. 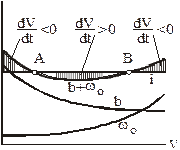Иная картина наблюдается при торможении на спуске. На рисунке изображены зависимости удельной тормозной силы b, основного удельного сопротивления w_o. Зависимости построены для случая торможения на спуске величиной i. Предположим, что результирующая сила w_o + b имеет две точки пересечения с линией w_i А и В. Точка А является точкой неустойчивого равновесия, так как при случайном изменении скорости в любую сторону появляется сила, равная w_b + b – i, которая способствует еще большему изменению скорости. Точка В является точкой устойчивого равновесия. Отсюда можно сформулировать условие устойчивости механического торможения: знаки отклонения скорости и ускорения, вызванного изменением замедляющей силы, должны быть противоположны.