10. Реализация силы тяги с учетом упругой деформации колеса и рельса.
Вследствие деформации колеса и рельса при взаимодействии, колесо в действительности опирается на рельс некоторой поверхностью. Процесс деформации очень сложен, а теоретические выражения, описывающие процесс взаимодействия колеса и рельса получены только для простейших случаев сочетания профилей колеса и рельса. Основу решения проблемы положил физик Г. Герц в 1882 г.
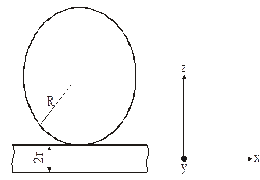
Рассмотрим идеализированный случай упругого взаимодействия колеса и рельса, полагая их материал изотропным. Начнем с неподвижного колеса. Расположим оси координат как показано на рисунке. Т.к. стандартный ж.д. рельс имеет в поперечном сечении радиус головки 300 мм, представим колесо и рельс в виде двух бесконечных цилиндров, расположенных во взаимно перпендикулярных плоскостях и имеющих, соответственно, радиусы R и r.Рассмотрим проекцию колеса на плоскость XOZ. Предположим, что под действием силы Gк произошла деформация колеса на величину z1. Длину проекции поверхности взаимодействия колеса и рельса на плоскость XOZ обозначим 2х. Рассмотрим треугольники АВО' и BОO'. Треугольники подобны, следовательно можно записать:
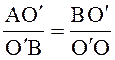 ;
;
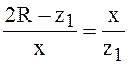 .
.
Так как z1 << R, то можно записать
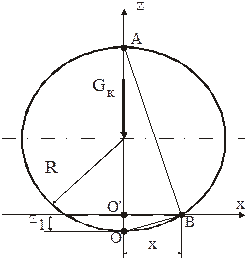
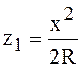
Рассматривая деформацию рельса в плоскости YOZ, по аналогии можно записать
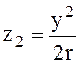 .
.
Суммарная деформация колеса и рельса
D = z1 + z2 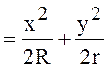 .
.
Это уравнение эллипса. Т.е. поверхность взаимодействия колеса и рельса при неподвижном колесе имеет форму эллипса. Величина эллипса зависит от:
- величины нагрузки колеса на рельс;
- модуля упругости материалов колеса и рельса;
- радиусов поверхностей взаимодействия колеса и рельса:
Распределение давления колеса на рельс имеет форму эллипсоида. Давление в произвольной точке эллипсоида равно:
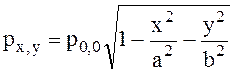 .
.
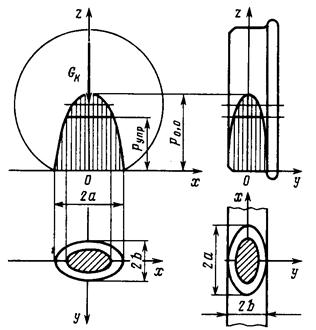 В центре эллипса (х = 0, у = 0) давление максимально
и равно
В центре эллипса (х = 0, у = 0) давление максимально
и равно
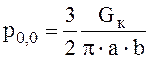 .
.
Для современных грузовых электровозов давление в центре эллипса в 1,5 раза больше среднего и у превышает предел упругости рупр колеса и рельса. Иными словами, в пределах заштрихованной площади происходят упругопластические деформации материалов колеса и рельса. Коническое очертание поверхности катания колеса и наклон поверхности катания рельса сильно усложняют решение задачи. Приближенно считают, что опорная поверхность в этом случае также имеет форму эллипса, площадь которого составляет 400-600 мм2. Меньшие значения площади соответствуют малым диаметрам колес и малым нагрузкам на ось. Ориентация эллипса и его размеры зависят от степени проката бандажа и износа рельса. При увеличении износа поверхность взаимодействия искажается и при изношенных бандаже и рельсе принимает форму, близкую к прямоугольнику, большая ось которого направлена поперек рельса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.