Расчет электрической цепи постоянного тока

Министерство путей сообщения Российской Федерации

Петербургский государственный Университет путей сообщения

 

Кафедра “Теоретические основы электротехники”

Домашнее задание №1

«Расчет электрической цепи постоянного тока»

Схема №19, вариант №3

Выполнил:

                                                                  Ст. группы______________    

________________________

Проверил:

________________________

Санкт-Петербург

2003

Содержание

1.  Условные обозначения…………………………………………………………..3

2.  Задание……………………………………………………………………………4

3.  Составление узловых и контурных уравнений цепи………………………….5

4.  Определение токов во всех ветвях ……………………………………………..7

5.  Определение показаний вольтметров…………………………………………..9

6.  Проверка баланса мощностей…………………………………………………..10

7.  Расчет потенциалов в точках соединения элементов внешнего контура.

      Построение потенциальной диаграммы……………………………….………11

8.   Нахождение тока в ветви с резистором R₁ методом эквивалентного

      источника.………………………………………………………………………..12

1. Условные обозначения

Е-ЭДС

I-сила тока в ветви.

J-ток источника тока.

      G-электрическая проводимость

      R-электрическое сопротивление

      U-напряжение    

      j-электрический потенциал точки схемы

      A – матрица соединений

      С – матрица контуров

2. Задание

Задана схема электрической цепи и численные значения ее параметров.

Требуется:

1.  Составить узловые и контурные уравнения цепи непосредственно по схеме.

2.  Определить токи во всех ветвях цепи.

3.  Определить показания вольтметров (сопротивления вольтметров принять равным бесконечности).

4.  Проверить баланс мощностей.

5.  Рассчитать потенциалы в точках соединения элементов внешнего контура и построить потенциальную диаграмму.

6.   Методом эквивалентного источника определить ток в ветви с резистором R_1.

                                       R₅                                                                                          R₇        

 

                                                                                                          G₀

J₀

                                                                 R₁

 

E₁

                              E₂              R₂                                                                              R₆

 

     R₃                                            E₃

 

                                                                                                                                   E₄

                               R₄

 

Рис.1

 Таблица 1

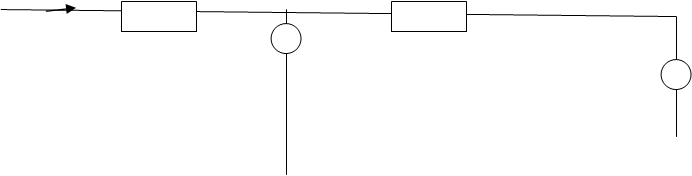
3.Составление узловых и контурных уравнений цепи

Составим узловые уравнения цепи, используя топологические матрицы. Изобразим граф схемы, представленной на рисунке 4 (стр. 7).

 

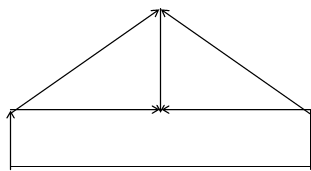
                                   Рис. 2

Составим матрицу соединений и, умножив её на вектор – столбец токов ветвей, получим узловые уравнения цепи.

 

                  0   1   2   3   5   6               I₀

            0    0  -1 -1   0   0 –1               I₁               -I₁ – I₂  - I₆

А * I = 1    0  0   1  -1   1   0      *        I₂       =     I₂ - I₃ + I₅     = 0  

            2   -1  1   0   0  -1   0                I₃                    -I₀ + I₁ – I₅

            3    1   0   0  1   0   1                I₅               I₀ + I₃  + I₆

                                                            I₆  

Составим контурные уравнения цепи, используя топологические матрицы. Изобразим граф схемы, представленной на рисунке 4 (стр. 7). В данном графе толстыми линиями обозначим дерево графа, а тонкими – линии связи.

 

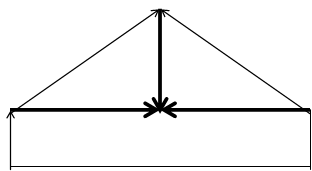                                   Рис. 3

Составим матрицу контуров и, умножив её на вектор – столбец напряжений ветвей, получим контурные уравнения цепи.

                  0   1   2   3   5   6               U₀

            0    1   1   0   0   0  -1               U₁               U₀ + U₁  - U₆

C*U = 3    0   0   1   1   0  -1        *     U ₂       =     U₂ + U₃  - U₆     = 0  

            5    0   1  -1  0   1   0                U₃                     U₁ – U₂  +U₅

                                                            U₅                                                                          

                                                            U₆

Запишем уравнения по первому и второму законам Кирхгофа непосредственно по схеме, представленной на рисунке 4.

Число уравнений по первому закону Кирхгофа равно числу независимых узлов, т.е. общее число узлов минус один. Так как всего на схеме четыре узла, число уравнений по первому закону Кирхгофа три. Пронумеруем узлы на схеме и запишем уравнения:

SI_k=0

Для узла 1:

I₂+I₅-I₃=0

Для узла 2:

      I₁-I₀-I₅=0

Для узла  3:

       I₀ +I₃+I₆=0

Число уравнений по второму закону Кирхгофа равно числу независимых контуров, т.е. общее число ветвей минус число независимых узлов. Для данной схемы это число равно трем.

   Пронумеруем контура, зададимся направлениями обхода и запишем уравнения по второму закону Кирхгофа:

Для контура  1:

       I₁R₁+I₅R₅-I₂R₂=E₁-E₂

Для контура  2:

       I₀(R₀+R₇)+I₁R₁-I₆R₆=E₀+E₁

Для контура  3:

       I₂R₂+I₃R₃-I₆R₆=E₂+E₃

 

4.Определение токов во всех ветвях методом узловых потенциалов

Изобразим исходную схему, исключив из нее ветви, содержащие вольтметры, так как сопротивление вольтметров равно бесконечности и по ним не течет ток. Преобразуем также источник тока в эквивалентный источник ЭДС.

Е₀=I₀/G₀=10.000000/0.400000=25.000000 (В)

R₀=1/G₀=1/0.400000=2.500000 (Ом)

                                       R₅                                        R₇                                        R₀

 

          E₀

                                                                 E₁

 

R₁

                        E₂                    R₂                                                                              R₆

 

     R₃                                            E₃