Электротехника \ Теоретические основы электротехники

Расчет электрической цепи постоянного тока, страница 2

Рис.4

Пронумеруем узлы схемы и найдем токи во всех ветвях по методу узловых потенциалов.

Пусть j₁=0, тогда система уравнений примет следующий вид:

φ₁(1/R₂+1/R₃+1/R₅)-φ₂/R₅-φ₃/R₃=E₃/R₃-E₂/R₂
-φ₁/R₅+φ₂(1/R₅+1/R₁+1/(R₀+R₇))-φ₃/(R₀+R₇)=E₀/(R₀+R₇)-E₁/R₁
-φ₁/R₃-φ₂/(R₀+R₇)+φ₃(1/R₃+1/(R₀+R₇)+1/R₆)=-E₀/(R₀+R₇)-E₃/R₃

φ₁(1/12.000000+1/8.000000+1/20.000000)-φ₃/20.000000-φ₃/8.000000=

=110.000000/8.000000-110.000000/12.000000
-φ₁/20.000000+φ₂(1/20.000000+1/15.000000+1/(2.500000+4.000000))-φ₃/(2.500000+

+4.000000)=25.000000/(2.500000+4.000000)-110.000000/12.000000
-φ₁/8.000000-φ₂/(2.500000+4.000000)+φ₃(1/8.000000+1/(2.500000+4.000000)+1/20.000000)=

=-25.000000/(2.500000+4.000000)-220.000000/15.000000

0.258333φ₁+-0.050000φ₂+-0.125000φ₃=4.583333
-0.050000φ₁+0.270513φ₂+-0.153846φ₃=-10.820513
-0.125000φ₁+-0.153846φ₂+0.328846φ₃=-17.596153

Решая систему уравнений, получаем:

φ₁=-82.585037 (B)
φ₂=-141.088455 (B)
φ₃=-150.907028 (B)

Зная потенциалы узлов схемы, найдем токи во всех ветвях:

I₀=(φ₂-φ₃+E₀)/(R₀+R₇)=(-141.088455--150.907028+25.00000)/(2.50000+4.0000)=2.335604 (A)

I₁=(φ₂-φ₀+E₁)/R₁=(-141.088455-0+220.000000)/15.000000=5.260770 (A)

I₂=(φ₁-φ₀+E₂)/R₂=(-82.585037-0+110.000000)/12.000000=2.284580 (A)

I₃=(φ₃-φ₁+E₃)/R₃=(-150.907028--82.585037+110.000000)/8.000000=5.209751 (A)

I₅=(φ₁-φ₂)/R₅=(-82.585037--141.088455)/20.000000=2.925171 (A)

I₆=(φ₃-φ₀)/R₆=(-150.907028-0)/20.000000=-7.545352 (A)

Проверим полученные значения с помощью уравнений Кирхгофа:

I₂+I₅-I₃=0
2.284580+2.925171-5.209751=0 0.000000=0

I₁-I₀-I₅=0
5.260770-2.335604-2.925171=0 -0.000005=0

I₀+I₃+I₆=0
2.335604+5.209751+-7.545352=0 0.000004=0

I₁*R₁+I₅*R₅-I₂*R₂=E₁-E₂
5.260770*15.000000+2.925171*20.000000-2.284580*12.000000=220.000000-110.000000
110.000000=110.000000

I₀*(R₀+R₇)+I₁*R₁-I₆*R₆=E₀+E₁
2.335604*(2.500000+4.000000)+5.260770*15.000000-

-7.545352*20.000000=25.000000+220.000000
245.000000=245.000000

I₂*R₂+I₃*R₃-I₆*R₆=E₂+E₃
2.284580*12.000000+5.209751*8.000000--7.545352*20.000000=110.000000+110.000000
220.000000=220.000000

Проверка с помощью законов Кирхгофа подтверждает правильность расчета.

5. Определение показаний вольтметров

Определим показание вольтметра V1 с помощью второго закона Кирхгофа:

I₆R₆+E₃= -7.545352 *20.000000+110.000000=-40.90704 (B)

Вольтметр V2 показывает разность потенциалов между точками 6 и 0 на схеме на рисунке 5 (см. пункт 7):

j₆-j₀=110.000000-0=110.000000 (B)

6. Проверка баланса мощности

Запишем уравнение баланса мощности:

I₀²(R₀+R₇)+I₁²R₁+ I₂²R₂+I₃²R₃+I₅²R₅+I₆²R₆ =I₀E₀+I₁E₁+ I₂E₂+I₃E₃

2.335604²*(2.500000+4.000000)+5.260770²*15.000000+2.284580²*12.000000+5.209751²*

*8.000000+2.925171²*20.000000=

=25.000000*2.335604+220.000000*5.260770+110.000000*2.284580+110.000000*5.209751

2040.136108=2040.135864

(2040.136108-2040.135864)/2040.136108*100=0.000012 (%)

Допустимая погрешность расчета 1-2 %. Полученная погрешность меньше допустимой, значит расчеты выполнены верно.

7. Расчет потенциалов в точках соединения элементов внешнего контура. Построение потенциальной диаграммы

Изобразим внешний контур исходной схемы и пронумеруем точки соединения элементов.

R₅ R₇ R₀

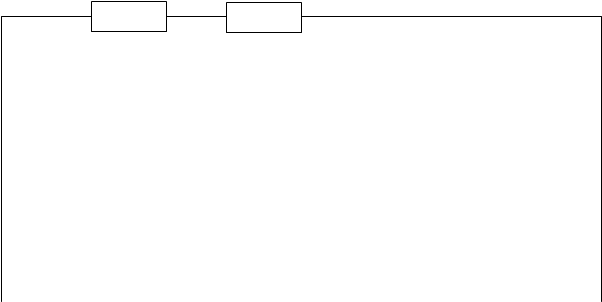E₀

R₃

R₄

E₄

E₃

Рис.5

Примем потенциал точки 0, соединенной с корпусом, равной нулю. Таким образом, получим:

j₀=0

φ₁=φ₀+E₄=0+220.000000=220.000000(В)

φ₂=φ₁-I₃R₃=220.000000-5.209751*8.000000=178.321991(В)

φ₃=φ₂-I₅R₅=178.321991-2.925171*20.000000=119.818573(В)

φ₄=φ₃+I₀R₇=119.818573+2.335604*4.000000=129.160995(В)

φ₅=φ₄+I₀R₀=129.160995+2.335604*2.500000=135.000000(В)

φ₆=φ₅-E₀=135.000000-25.000000=110.000000(В)

φ₁=φ₆+E₃=110.000000+110.000000=220.000000(В)

По полученным значениям построим потенциальную диаграмму.

8.Расчет тока в ветви с резистором R₁ методом эквивалентного источника

Определим ток в ветви с резистором R₁методом эквивалентного источника ЭДС. Изобразим исходную схему, исключив из нее ветвь с резистором R₁, и найдем напряжение холостого хода.

R₅ R₇ R₀

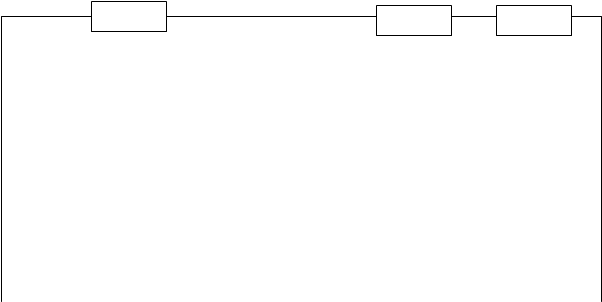E₀

U_xx

E₂ R₂R₆

R₃E₃

Рис.6

I_I(R₀+R₂+R₅+R₆+R₇)+I_II(R₂+R₆)=E₀+E₂
-I_I(R₂+R₆)+I_II(R₂+R₃+R₆)=E₂+E₃

I_I(2.500000+12.000000+20.000000+20.000000+4.000000)+I_II*(12.000000+20.000000)=

=25.000000+110.000000
I_I(12.000000+20.000000)+I_II(12.000000+8.000000+20.000000)=110.000000+110.000000

58.500000I_I+32.000000I_II=135.000000
32.000000I_I+40.000000I_II=220.000000

Решая систему уравнений, получим:

I_I=-1.246201 (A) I_II=6.496961 (A)

I₅=I_I=-1.246201 (A)
I₂=I_I+I_II=-1.246201+6.496961=5.250760 (A)

U^mn_xx+I₂R₂+I₅R₅=E₂

U^mn_xx=E₂-I₂R₂-I₅R₅

U^mn_xx=25.000000-5.250760*12.000000--1.246201*20.000000

U^mn_xx=71.914886 (B)

Найдем внутреннее сопротивление эквивалентного источника ЭДС:

R₀

R₆

R₇

R₃

R₅

R₂

Рис. 7

Преобразуем треугольник в звезду:

R₃₆R₀R₇

R₂₆ R₅ R₂₃

Рис. 8

R₂₆=R₂*R₆/(R₂+R₃+R₆)
R₂₆=12.000000*20.000000/(12.000000+8.000000+20.000000)=6.000000 (Ом)

R₂₃=R₂*R₃/(R₂+R₃+R₆)
R₂₃=12.000000*8.000000/(12.000000+8.000000+20.000000)=2.400000 (Ом)

R₃₆=R₃*R₆/(R₂+R₃+R₆)
R₃₆=8.000000*20.000000/(12.000000+8.000000+20.000000)=4.000000 (Ом)

R₀₃₆₇=R₀+R₃₆+R₇R₀₃₆₇=2.500000+4.000000+4.000000=10.500000

R_mn=R₀₃₆₇*(R₂₃+R₅)/(R₀₃₆₇+R₂₃+R₅)+R₂₆
R_mn=10.500000*(2.400000+20.000000)/(10.500000+2.400000+20.000000)+6.000000=

=13.148936 (Ом)

Найдем ток в ветви с резистором R₁:

I₁=(E₁-U^mn_хх)/(R_вн^mn+R₁)

I₁=(220.000000-71.914886)/(15.000000+13.148936)=5.260771 (А)

Значение тока I₁, полученное по методу эквивалентного источника ЭДС, совпадает со значением, полученным по методу узловых потенциалов.

1 2

Скачать файл