Цель работы: освоение методов моделирования случайных процессов и последовательностей с заданными спектрально-корреляционными свойствами.
При моделировании систем управления и обработки информации важно уметь формировать модели внешних воздействий и ошибок измерений, представляемых, как правило, стационарными процессами с заданными корреляционными функциями R(t) или спектральными плотностями S(w). Как известно, данные статистические характеристики связаны между собой прямым и обратным преобразованиями Фурье:
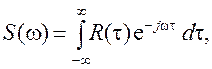
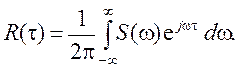
Для того чтобы сформировать стационарный процесс с заданными свойствами обычно используют метод формирующего фильтра, рассчитывая его таким образом, чтобы при подаче на вход фильтра процесса x(t) типа белого шума его выходной сигнал y(t) обладал указанными характеристиками. Для получения передаточной функции формирующего фильтра Wфф(p) спектральную плотность моделируемого процесса повергают факторизации, т.е. представляют ее в виде произведения двух комплексно сопряженных сомножителей, все нули и полюса первого из которых лежат в левой полуплоскости, а второго – в правой:
![]()
Здесь предполагается, что интенсивность порождающего белого шума x(t) равна единице.
Модель формирующего фильтра, заданная его передаточной функцией, может быть также представлена в форме пространства состояний [1]:
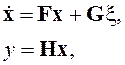 (1)
(1)
где x – вектор состояния фильтра; F – матрица динамики; G – матрица возмущений; H– матрица наблюдения.
Начальное состояние фильтра x(0) должно быть сформировано таким образом, чтобы обеспечить стационарность выходного процесса. Это условие выполняется, если ковариационная матрица P вектора состояния в начальный момент времени соответствует ее установившемуся значению, которое может быть найдено из уравнения [2]
![]() (2)
(2)
Поскольку при компьютерном моделировании случайный процесс неизбежно должен быть представлен своими дискретными отсчетами, от непрерывной модели (1) переходят к ее дискретному описанию [1]:
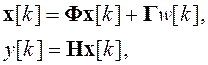 (3)
(3)
где w[k] – дискретный белый шум. Параметры дискретной модели в первом приближении могут быть определены из соотношений
F = E + FT, G = BT, Q = 1/T, (4)
где Q – дисперсия шума w[k]; T – период дискретности; E – единичная матрица. При этом период дискретности T следует выбирать таким образом, чтобы он был много меньше, чем время затухания корреляционной функции моделируемого процесса.
Проведем математическое моделирование недифференцируемого узкополосного марковского процесса второго порядка. Корреляционная функция и спектральная плотность такого процесса соответственно имеют вид
![]() , (5)
, (5)
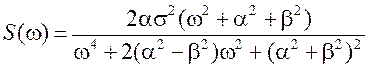 . (6)
. (6)
Здесь параметр a представляет собой ширину спектра, параметр b – преобладающую частоту процесса.
Осуществим факторизацию спектральной плотности (6). Для этого преобразуем выражение в знаменателе, представив его в виде произведения комплексно сопряженных сомножителей:
![]()
![]()
![]()
Тогда можно записать
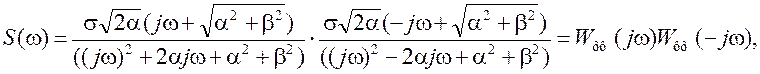
откуда получим
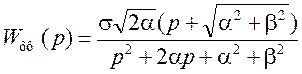 .
.
Считая белый шум x(t) входом формирующего фильтра, а моделируемый процесс y(t) – его выходом, запишем дифференциальное уравнение
![]() . (7)
. (7)
Представим динамическую систему (7) в управляемой канонической форме [1]:
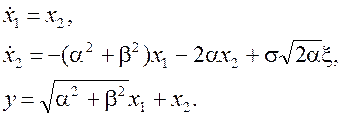
Переходя к векторно-матричной записи
уравнений в виде (1), определим 
![]()
![]()
Решением матричного уравнения (2) получим ковариационную матрицу вектора состояния
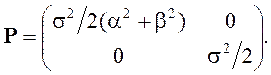
Эквивалентная дискретная модель формирующего фильтра может быть получена с использованием соотношений (4). При этом период дискретности выберем равным T = 0,001¸0,01 a–1.
Текст m-файла, реализующего рассмотренный алгоритм моделирования, представлен в Приложении.
1. Получить вариант задания у преподавателя.
2. Получить выражения для формирующих фильтров в форме передаточной функции и в форме пространства состояний. Записать входящие в эти выражения матрицы F, G, H и P с учетом выполнения условия стационарности процесса.
3. С учетом выполнения условия стохастической эквивалентности записать выражения для матриц F, G, Q дискретной системы с точностью до членов первого порядка. Задать величину периода дискретности T.
4. Используя Matlab, составить программу, обеспечивающую получение реализаций моделируемого процесса. Построить график выборочной корреляционной функции.
Табл. 4.1. Варианты заданий
|
Вариант |
R(t) |
S(w) |
s |
a, с–1 |
b, с–1 |
|
1 |
|
|
1 |
0,5 |
2 |
|
2 |
|
|
2 |
2 |
– |
|
3 |
|
|
3 |
1 |
– |
|
4 |
|
|
4 |
1 |
– |
|
5 |
|
|
5 |
0,5 |
2 |
Отчет о лабораторных исследованиях должен содержать:
- исходные данные;
- непрерывную модель формирующего фильтра в форме передаточной функции и в форме пространства состояний;
- параметры эквивалентной дискретной модели;
- текст m-файла, с помощью которого получены реализации моделируемого процесса;
- графики теоретической и выборочной корреляционных функций;
- выводы по работе.
1. Какие случайные процессы называются стационарными?
2. Перечислите основные статистические характеристики стационарных случайных процессов. Как они связаны между собой?
3. Что называют формирующим фильтром?
4. Поясните процедуру факторизации.
5. Каковы основные методы получения описания динамической системы по заданной передаточной функции?
6. Как следует задавать начальное состояние формирующего фильтра при моделировании стационарных процессов?
7. Опишите процедуру получения эквивалентной дискретной модели фильтра по имеющейся непрерывной модели.
8. Как следует выбирать период дискретности при компьютерном моделировании стационарных случайных процессов?
9. Поясните, почему моделируемые в работе случайные процессы можно называть марковскими. В каком смысле их можно назвать марковскими процессами первого порядка?
10. Поясните, как по имеющейся реализации построить график выборочной корреляционной функции.
1. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке MATLAB. – СПб.: Наука, 1999. – 467 с.
2. Степанов О.А. Применение теории нелинейной фильтрации в задачах обработки навигационной информации. – СПб: ГНЦ РФ – ЦНИИ «Электроприбор». – 1998. – 370 с.
Текст m-файла к примеру выполнения работы
clear; close all;
N = 200000; %число отсчетов случайного процесса
M = N/200; %число отсчетов корреляционной ф-ии
%Параметры случайного процесса
sig = 1.5;
alf = 0.5;
bet = 2;
dt = 0.01; %период дискретности
%Формирование непрерывной модели динамики
F = [0 1; -(alf^2 + bet^2) -2*alf];
G = [0; sig*sqrt(2*alf)];
H = [sqrt(alf^2 + bet^2) 1];
%Дискретизация непрерывной модели
Fi = eye(2) + F*dt;
Gam = G*dt;
%Формирование начального состояния фильтра
P = [sig^2/2/(alf^2 + bet^2) 0; 0 sig^2/2];
x = sqrt(P)*normrnd(0,1,2,1);
%Формирующий фильтр
y(N) = 0;
w = normrnd(0,1/sqrt(dt),1,N);
for k = 1:N
x = Fi*x + Gam*w(k);
y(k) = H*x;
end;
%Обработка результатов моделирования
t = (-M:M)*dt;
r2 = sig^2*exp(-alf*abs(t)).*cos(bet*t);
%теоретическая корреляционная ф-ия
R2 = xcov(y,'unbiased');
%выборочная корреляционная ф-ия
m1 = 1:N;
figure;
plot(m1*dt,y);
xlabel('t,c');
title('Реализация случайного процесса');
figure;
plot(t,R2(N-M:N+M));
hold on;
plot(t,r2,'r--');
xlabel('\tau, c');
ylabel('R(\tau)');
title('Корреляционная функция');
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.