Рассмотрим принципы построения сверточных кодов. При использовании блочных (n ,к )-кодов для формирования кодовых символов последовательность поступающих информационных символов разбивается на блоки по к информационных символов в каждом, которые в результате кодирования преобразуются в n кодовых символов, составляющих кодовое слово, причем кодовые слова формируются независимо друг от друга. Наряду с блочными кодами в системах передачи информации применяются и непрерывные коды,в частности рекуррентные коды.При рекуррентном кодировании разбиение кодируемой последовательности информационных символов на блоки не производится, а кодовые символы вычисляются последовательно по мере поступления информационных символов по некоторым рекуррентным соотношениям, выбранным для данного .типа кода. Если эти рекуррентные соотношения линейные,то получаемый рекуррентный код называется сверточным, поскольку формируемые при этом кодовые символы можно представить в виде свертки последовательности информационных символов и порождающего многочлена кода, задающего линейные рекуррентные правила кодирования.
Для рекуррентных кодов, в частности для сверточных, понятие кодового слова не имеет смысла, так как кодовые символы вычисляются по текущему блоку последних информационных символов для каждого такта работы кодирующего устройства. Поэтому подобные коды называют также цепными.
Практическая ценность рассматриваемых ниже сверточных кодов обусловлена широким распространением каналов передачи информации, в которых преобладают импульсные помехи, вызывающие искажение целого ряда следующих друг за другом символов.
В случае двоичных сверточных кодов рекуррентная формула для определения качества символов кодовой последовательности принимает вид
|
где J.=0,1,..., I -1;
Сnо. = 0 или I;
Ьi - символы входной информационной последовательности. Структурная схема кодирующего устройства несистематического сверточного кода, обеспечивающего формирование символов по правилу (6.89), изображена на рис.13.6. Символы входной информационной последовательности поступают на регистр сдвига, содержащий К = S + q ячеек, которым в соответствии присвоены номера от -0 до s - I. Символы b ij формируются с помощью сумматоров М2 (осуществляющих суммирование по mod 2), на которые с ячеек регистра сдвига, отвечающих ненулевым значениям Сnо. поступают информационные символы. В тот такт работы регистра сдвига, когда в нулевой его ячейке находится символ bi. (соответственно во входной ячейке-символ bi+s-i , а в выходной - символ bi-q ), на сумматорах формируются символы b.,. . Коммутатор в i-м такте работы регистра сдвига, в течение которого остаются неизменными заполняющие его символы Ьi. , поочередно выдает в канал связи символы bij.
В следующем такте все символы в регистре сдвигаются вправо на одну ячейку: в нулевой ячейке находится символ Ьi+1, , во входной - символ bi+s , а в выходнойbi-q+1.
Соответственно на сумматорах формируются символы кодовой последовательности В. ;
На рис.13.6 изображена структурная схема кодирующего устройства систематического сверточного кода. Здесь отличие от несистематического кода состоит в том, что на один из входов
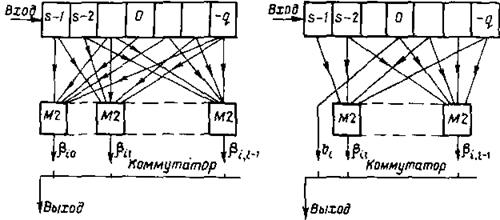
Рис.13.6 Рис.13.7
коммутатора (например, на первый) непосредственно из нулевой ячейки сдвигающего регистра поступает символ bi .
Основное отличие сверточного кода от блочных систематических кодов здесь состоит в непрерывном обновлении группы информационных символов, участвующих в формировании очередных I символов выходной кодовой последовательности. При блочном кодировании формирование всех символов данного кодового слова происходит с использованием одного и того же блока информационных символов, который целиком обновляется при переходе к кодированию следующего слова.
Это создает принципиальную возможность, используя несистематические коды, получать выигрыш в эффективности кода благодаря тому, что в несистематическом коде все символы кодовой последовательности (а не только избыточные) участвуют в коррекции ошибок. Однако практическая реализация этого выигрыша возможна лишь при создании алгоритмов декодирования, вычислительная сложность которых не превышала бы возможностей используемых вычислителей.
В самом общем виде схема декодирования сверточных кодов произвольной структуры представляется следующей. Декодирование заключается в отборе наиболее правдоподобных из них по отношению к принятой кодовой последовательности, например по метрике Хемминга, т.е. по кодовому расстоянию.. Поэтому для создания реализуемых вариантов декодирования несистематических еверточных кодов произвольной структуры необходимо найти такой подход к решению задачи, который позволил бы сократить объем перебора
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.