Помехоустойчивое кодирование командно-программной информации, страница 5

Коды Хемминга представляют собой простейшую разновидность циклических кодов. Как уже отмечалось, существуют коды Хемминга с кодовым расстоянием d = 2,3 и 4. Код, у которого  d = 2, является блочным циклическим кодом типа (п , п -I), осуществляющим проверку п -значных кодовых комбинаций на четность. Кроме обнаружения одиночных ошибок этот код позволяет также обнаруживать и другие ошибки нечетной кратности.

Правило, по которому осуществляется формирование показания последнего разряда (с номером п ) кодовой комбинации, записывается в следующем виде:

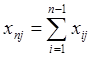где j. - номер слова (кодовой комбинации);

I - номер разряда в пределах кодовой комбинации;

Х_ij. - показание ("О" или "I") каждого разряда данного слова.

Код Хемминга с кодовым расстоянием d = 3, являющийся циклическим (n , к)-кодом, на практике используется для обнаружения и исправления одиночных ошибок. Для этого кода количество проверочных символов n - к  >8

Здесь двоичное число, составленное из контрольных сумм(по mod  2) и называемое синдромом кода, должно определять порядковый номер искаженного разряда кодового слова. Для этого контрольные суммы составляются так, чтобы в сумму S.   входили символы кодового слова, имеющие единицу в  l -м разряде двоичной записи их порядкового номера в пределах  п -разрядной кодовой комбинации. При этом символы, порядковый номер которых в двоичной записи выражается только одной единицей в I -м разряде, т.е. равен 2^1-1    , войдут только в одну контрольную сумму S_i  . Именно на этих позициях (I, 2, 4, 8-й и т.д.) в коде Хемминга и располагаются проверочные символы b₁, b_2, , b_4,. b₈.. Соответствующим их выбором, т.е. приписыванием им нуля или единицы, все контрольные суммы при кодировании должны обращаться в нуль. При отсутствии искажений в канале связи все контрольные суммы, сформированные при приеме данной кодовой комбинации,останутся равными нулю. Одиночная ошибка, например искажение  l -го разряда передаваемого кодового слова, приведет к обращению в единицу контрольных сумм, номера которых соответствуют номерам разрядов двоичной записи числа i , содержащих единицы. Поэтому, записывая в виде двоичного числа значения контрольных сумм в порядке убывания их номеров, т.е. формируя синдром вида .S ₈ S₄S₂S₁. , получаем в двоичной записи номер /  искаженного разряда.

Для наглядности рассмотрим двоичную запись номеров разрядов 15-разрядного числа (табл.6.5), используемого в коде Хемминга (15,11). В данном коде используется n- к = 4 проверочных символа b₁, b_2, , b_4,. b₈ располагаемых в кодовой комбинации на местах с номерами

I= I, 2, 4, 8.

Таблица 13.2

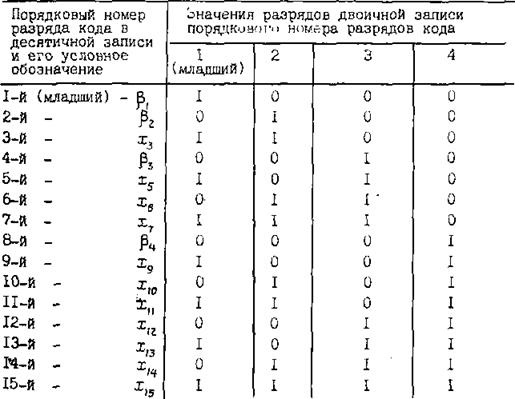
Для 15-разрядного кода в соответствии с табл.13.3 составляются контрольные суммы

Х-   - значения одиннадцати информационных символов кода;

b₁, b_2, , b_4,. b₈.- значения проверочных символов

Значения проверочных символов b₁, b_2, , b_4,. b₈ должны выбираться таким образом,чтобы обратить в нуль контрольные суммы.

Таким образом, процедура кодирования информации включает следующие операции:

- расположение информационных символов в порядке возрастания разрядов с сохранением свободными разрядов, имеющих номера 2^i-1 ;

- вычисление значений проверочных символов и расположение их на позициях с номерами 2^i-1

При декодировании информации выполняются следующие операции:

- вычисление контрольных сумм по формулам

- определение порядкового номера искаженного символа (выполняется в результате анализа синдрома) и исправление его;

- выдача потребителю к  информационных символов кодовой комбинации (выдаются разряды за исключением тех из них, номера которых равны  2^i-1  .

Коды Боуза - Чоудхури - Хоквингема (БЧХ) являются обобщением кодов Хемминга на случай исправления нескольких ошибок. Они образуют наилучший среди всех известных класс блочных (n ,к )-кодов для каналов, в которых искажения отдельных символов возникают независимо.

CВЕРТОЧНЫЕ КОДЫ