Равномерные блочные коды бывают разделимыми и неразделимыми. Разделимым является код, в котором символы разделены на информационные и проверочные. При этом места информационных и проверочных символов в кодовой комбинации заранее определены. В неразделимых кодах деление на информационные и проверочные символы отсутствует.
Примером неразделимых кодов являются коды с постоянным весом.
Под кодом с постоянным весом обычно понимают двоичный равномерный код, в котором разрешенные комбинации содержат одинаковое число единиц. Такой код обеспечивает обнаружение всех ошибок, за исключением тех случаев, когда несколько единиц превратятся в нули, а столько же нулей - в единицы. Эти ошибки называют ошибками смещения.
Основным достоинством кодов с'постоянным весом является их высокая помехоустойчивость в асимметричных каналах, в которых вероятности искажения единиц и нулей различные.
В системах передачи информации с импульсным излучением широкое распространение получили так называемые позиционно-импульсные коды, в которых различные кодовые комбинации содержат постоянное число импульсов: Эти коды также являются кодами с постоянным весом. Здесь наличие импульса в определенной тактовой точке ti временной оси (рис.13.3) можно рассматривать как единичный сигнал, а его отсутствие - как нулевой сигнал.

рис 13.3
Максимальное число сообщений, которые можно закодировать с помощью описанных кодов с постоянным весом, равно Np= Сnk ,где n - общее число символов кода (тактовых точек), к - число единичных символов (импульсов) кода.
Кодом с постоянным весом является и так называемыйбиимпульсный код. Кодирование в этом случае состоит в том, что символы 0 и I подлежащей передаче информации (рис.13.4,а) кодируются соответственно в виде сочетаний 01 и 10 символов канала связи (рис.13.4б). Этот код обнаруживает все ошибки, за исключением тех случаев, когда в одной паре символов канала связи, соответствующих данному информационному разряду, исказились оба символа. Другим достоинством биимпульсного кода является надежная посимвольная синхронизация,
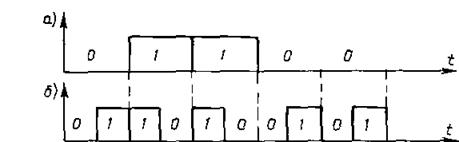
Рис.13.4
поскольку в канале связи в течение длительности информационного символа происходит смена качества символов канала связи. Недостатком биимпульсного кода является расширение требуемой полосы частот канала связи. Биимпульсные коды находят применение в системах передачи информации с непрерывным излучением.
Широкое применение в практике передачи информации нашли систематические блочные коды. Наиболее известны среди них циклические коды. Коды Хемминга являются разновидностью циклических кодов, но исторически появились раньше многих других ныне известных кодов и сыграли большую роль в развитии теории помехоустойчивого кодирования. Другой важной разновидностью циклических кодов являются коды Боуза - Чоудхури - Хоквингема (БЧХ). Остановимся подробнее на общих принципах построения циклических кодов, выделив отдельно коды Хемминга и БЧХ-коды.
ЦИКЛИЧЕСКИЕ КОДЫ
Циклические коды отличаются высокой эффективностью обнаружения ошибок и сравнительной простотой реализации кодирующих и декодирующих устройств. Название этого класса кодов произошло от основного их свойства, заключающегося в том, что в результате циклической перестановки символов одной кодовой комбинации кода можно получить новые комбинации этого кода.
Циклические коды достаточно часто описываются с использованием многочленов переменной х . Цифры двоичного кода рассматриваются как коэффициенты многочлена. Например, записанное в двоичном коде сообщение IOOIIOI может быть представлено многочленом вида 1•х6 + 0•xs+ О•x4+ 1•х3 + I •x2+ 1•-х°= =х6 + х3 + х2 + I. При таком представлении кодов математические операции с полученными многочленами производятся в соответствии с законами общей алгебры, за исключением того, что .сложение осуществляется по mod 2.
Принцип обнаружения ошибок при помощи циклического кода заключается в том, что в качестве разрешенных принимаются кодовые комбинации, описывающие многочлены которых G-(x) делятся без остатка на некоторый заранее выбранный исходный (образующий) многочлен Р(х) . Если принятая комбинация искажена, то это условие на приемной стороне не выполняется, в результате чего фиксируется факт ошибки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.