Помехоустойчивое кодирование командно-программной информации, страница 2

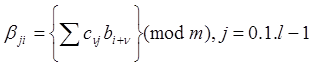
Значение правой части определяется по mod m  .что означает, что после проведения обычных вычислительных операций удерживается лишь остаток от деления полученной величины на основание кода m (например, 7 по  mod 4 дает 3). Суммирование необходимо для сохранения алфавита (разрядности).

Код Хеминга блочный равномерный групповой код, позволяет корректировать однократные ошибки. В основе кода лежит проверка на четность

Код формируется так. а₁ а2a3 а4 a5 a6 a7

№ проверки	Проверенные  позиции	Контрольные поз.
1	1 3 5 7 9 11 13 15 17	1 (а1)
2	2 3 6 7 10 11 14 15 18	2 (а2)
3	4 5 6 7 12 13 14 15 20	4 (а3)
4	8 9 10 11 12 13 14 15 24	8 (а4)

n=5 к=2 а1=a2+a1  а2=a2  а3=a1

Декодирование а1+a2+a1=0(1)  а2+a2=0(1),     а3+a1=0(1)

Равномерные блочные  коды бывают разделимыми и неразделимые.

Разделимые коды символы разделены на информационные и проверочные.

Циклические коды в основе многочлены переменной х. Коэффициенты многочленов – сообщение. Обнаружение ошибок –используются коды многочлены котрорых делятся без остатка на заранее выбранный многочлен.

Сверочные коды. При использовании блочных (n,к) кодов для формир кодовых символов последовательность поступающих инф. Символов разбивается на блоки  по к информационным символам которые в результате кодирования преобразуются в n символов, причем кодовые слова формируются независимо. Кодовые символы вычисляются по текущему блоку последних информационных символов для каждого такта работы кодир устройства. Поэтому эти коды наз. цепными.

Таким образом, удается резко увеличить помехозащищенность каналов связи.

Рассмотрим эти коды подробнее.

Соотношения d устанавливают связь между кодовым расстоянием и кратностью обнаруживаемых и исправляемых ошибок. В табл.12.3  на основе этих соотношений показаны возможности различных кодов в зависимости от величины кодового расстояния d.

Определим количество проверочных разрядов, необходимое для исправления ц   ошибок. Для этого необходимо, чтобы с помощью проверочных разрядов можно было описать следующие возможные ситуации:

1) ошибка отсутствует в  С_n° = I случае;

2) одиночная ошибка возникает в  С_n'   случаях;

3) двойная ошибка возникает в  С²_n-   случаях;

4) ошибка кратности m_n возникает в С^m_n случаях. Необходимо с помощью п - k  проверок выявить какую-то из этих ситуаций и результат представить в виде двоичного номера этой ситуации. Таким образом, количество проверочных разрядов п - k для исправления ошибок кратности m_n и менее определяется из неравенства

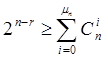       (13.3)

Соотношением (13.3) можно воспользоваться и при нахождении числа проверочных элементов для обнаружения ошибок. В этом случае необходимо использовать тот факт, что для данного кодового расстояния d  число обнаруживаемых ошибок m₀ в два раза больше числа исправляемых ошибок, т.е. m₀ =2m_и.

Практически количество избыточных разрядов может быть больше.

Пример. Пусть число информационных разрядов

k = 10, а кратность обнаруживаемых ошибок m₀ =5. Необходимо определить минимальное значение общего числа разрядов кода n.  Поскольку кратность обнаруживаемых ошибок нечетная, то, воспользовавшись соотношением 13.3 получим:

(n-10)> 1+ log(1+C_n¹+C_n²)

Последнее неравенство при сравнительно небольших значениях л и k удобно решать путем подбора неизвестных, ближе всего удовлетворяющих подобным неравенствам. В рассматриваемом примере неравенство удовлетворяется, а начиная с п= 19 .

Коды с d = 3 и 4, которые позволяют обнаруживать и исправлять одиночные ошибки или обнаруживать двойные и исправлять одиночные ошибки, в литературе обычно называют кодами Хемминга.

Например, если необходимо обнаруживать ошибки кратности m=1,то  величина (п -k ) > I. Таким  кодом,  в  частности,  является  код,  осуществляющий проверку  кодовых  комбинаций  на  четность (нечетность) единичных или нулевых символов. У такого кода  кодовое расстояние равно 2, а общее число символов на единицу превышает число информационных символов, т.е. соблюдается равенство  п = k + I. Этот код обнаруживает все одиночные ошибки, но он же может обнаружить любое нечетное число ошибок (3, 5, 7 и т.д.), кратность которыхm₀> d