Измерения в радиоэлектронике: Методические указания к лабораторным работам, страница 8

7. Строится гистограмма. Для этого по оси результатов наблюдений в порядке возрастания номеров откладываются интервалы  и на каждом интервале строится прямоугольник, высота которого пропорциональна .

По результатам анализа гистограммы высказывается гипотеза о виде закона распределения экспериментальных данных и о численных характеристиках этого закона (для нормального распределения такими характеристиками являются математическое ожидание и дисперсия). После этого используют критерий согласия для проверки гипотезы.

Критерий согласия  Пирсона имеет вид [2]

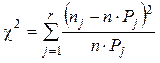, где величина  характеризует меру отклонения результатов наблюдений от теоретически предсказанных,  – частость попадания результатов наблюдений в j-й интервал,  – теоретические значения вероятности попадания результатов в j-й интервал, которые вычисляются по формуле

, где  – функция Лаплас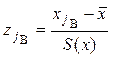а, , а .

После вычисления значения  для заданного уровня значимости  и числа степеней свободы  по таблицам -распре-деления находят критическое значение критерия согласия . Число степеней свободы рассчитывают по формуле

,                                        (2)

где  – количество интервалов разбиения,  – число параметров, необходимых для определения теоретической функции распределения (для нормального закона распределения ).

В технической практике обычно задаются уровнем значимости  = 0,05. Значения  для этого уровня значимости приведены в табл. 7.

Если , то принимают гипотезу о том, что результаты наблюдений принадлежат нормальному распределению, характеризующемуся математическим ожиданием и дисперсией. В противном случае, если , гипотеза отвергается.

Вычисление доверительных границ случайной погрешности результата измерения. Доверительные границы случайной погрешности результата измерения  (без учета знака) находят по формуле

, где  – квантиль распределения Стьюдента, который зависит от доверительной вероятности  и числа наблюдений . Значения величины  приведены в табл. 8.

Т а б л и ц а  8

Значения квантиля распределения Стьюдента

	0,75	0,875	0,95	0,975	0,99	0,995
16	0,690	1,194	1,746	2,120	2,583	2,921
17	0,689	1,191	1,740	2,110	2,567	2,898
18	0,688	1,189	1,734	2,101	2,552	2,878
19	0,688	1,187	1,729	2,093	2,539	2,861
20	0,687	1,185	1,725	2,086	2,528	2,845
21	0,686	1,183	1,721	2,080	2,518	2,831
22	0,686	1,182	1,717	2,074	2,508	2,819
23	0,685	1,180	1,714	2,069	2,500	2,807
24	0,685	1,179	1,711	2,064	2,492	2,797
25	0,684	1,178	1,708	2,060	2,485	2,787
26	0,684	1,177	1,706	2,056	2,479	2,779
27	0,684	1,176	1,703	2,052	2,473	2,771
28	0,683	1,175	1,701	2,048	2,467	2,763
29	0,683	1,174	1,699	2,045	2,462	2,756
30	0,683	1,173	1,697	2,042	2,457	2,750
40	0,681	1,167	1,684	2,021	2,423	2,704
50	0,679	1,164	1,676	2,009	2,403	2,678
100	0,677	1,157	1,660	1,984	2,364	2,626
	0,674	1,150	1,645	1,960	2,326	2,576