Измерения в радиоэлектронике: Методические указания к лабораторным работам, страница 7

Кол-во степеней свободы	Уровень значимости
	0,01	0,05	0,1
1	0,00016	0,00393	0,0158
2	0,0201	0,103	0,211
3	0,115	0,352	0,584
4	0,297	0,711	1,06
5	0,554	1,15	1,61
6	0,872	1,64	2,2
7	1,24	2,17	2,83
8	1,65	2,73	3,49
9	2,09	3,33	4,17
10	2,56	3,94	4,87
11	3,05	4,57	5,58
12	3,57	5,23	6,3
13	4,11	5,89	7,04
14	4,66	6,57	7,79
15	5,23	7,26	8,55

2. При определении доверительных границ погрешности результата измерения значение доверительной вероятности  принимают равной 0,95.

3. В тех случаях, когда измерения нельзя повторить, помимо доверительных границ, соответствующих вероятности , допускается указывать границы для .

Вычисление среднего арифметического ряда наблюдений.Среднее арифметическое ряда наблюдений (результатов наблюдений) рассчитывают по формуле

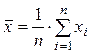, где – среднее арифметическое ряда наблюдений,  – i-й результат наблюдения,  – число результатов наблюдений.

Вычисление оценки среднего квадратического отклонения ряда наблюдений.Среднее квадратическое отклонение ряда наблюдений  рассчитывают по формуле

.

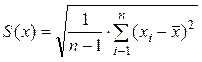Оно является основной характеристикой размера случайных погрешностей результатов наблюдений.

Вычисление среднего квадратического отклонения результата измерения.Для расчета среднего квадратического отклонения результата измерения  используется формула

.

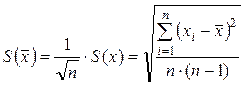Проверка гипотезы о принадлежности результатов наблюдений нормальному распределению. Чтобы установить, принадлежат (или не принадлежат) результаты наблюдений тому или иному распределению, необходимо сравнить экспериментальную функцию распределения с предполагаемой теоретической. Сравнение осуществляется с помощью критериев согласия.

В случае проверки принадлежности результатов наблюдений к нормальному распределению предпочтительным, при числе результатов , является один из критериев:  Пирсона или  Мизеса – Смирнова. В настоящей работе используется критерий Пирсона.

При числе результатов наблюдений  производят приближенную проверку их принадлежности к нормальному распределению путем оценки коэффициента асимметрии и эксцесса.

При  гипотеза о принадлежности результатов наблюдений к какому-либо распределению не проверяется. Если при этом имеется априорная информация о том, что нет причин, которые могли бы вызвать заметное отклонение распределения результатов от нормального закона, для обработки результатов наблюдений используется распределение Стьюдента.

Для проверки принадлежности результатов наблюдений к нормальному распределению с помощью критерия согласия Пирсона необходимо сначала построить гистограмму.

Построение гистограммы включает в себя следующие этапы.

1. Результаты наблюдений располагаются в порядке возрастания: , ,…, , где .

2. Вычисляется диапазон изменения значений результатов наблюдений: .

3. Весь этот диапазон разбивается на  интервалов одинаковой ширины. Необходимое количество интервалов разбиения можно оценить по формуле

                                     (1)

с последующим округлением в большую сторону до ближайшего целого нечетного числа (обычно  лежит в диапазоне от 7 до 15).

4. Определяется ширина интервала: .

5. Определяются границы интервалов  так, чтобы верхняя граница j-го интервала , а нижняя граница совпадала с верхней границей (j-1)-го интервала: .

6. Для каждого j-го интервала (j = 1,2,..., ) вычисляются числа  – частость попадания результата наблюдений в j-й интервал.