Составление и расчет размерных цепей

Составление и расчет размерных цепей.

Размерной цепью называют совокупность взаимосвязанных размеров, образующих замкнутый контур и определяющих взаимное расположение поверхностей одной или нескольких деталей.

В первом случае размерную цепь называют детальной, во втором – сборочной.

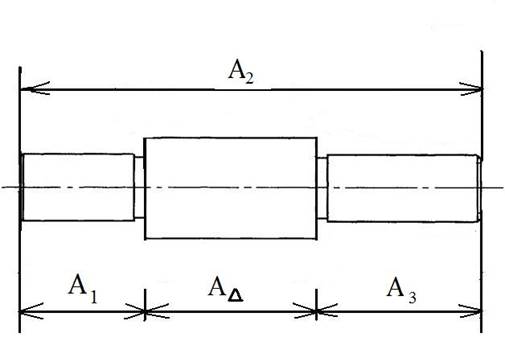
Деталь

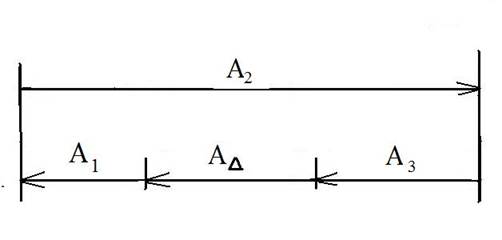
Схема детальной размерной цепи (рис. 1).

Размеры, образующие размерную цепь, называют звеньями и обозначают прописными буквами с индексами.

Звено, получаемое последним в результате изготовления детали или сборки, называют замыкающим или исходным и обозначается с индексом «∆».

В сборочной размерной цепи замыкающим звеном обычно является зазор.

При составлении схемы размерной цепи звенья представляются в виде векторов произвольной длины без соблюдения масштаба, которые откладываются на двух параллельных линиях.

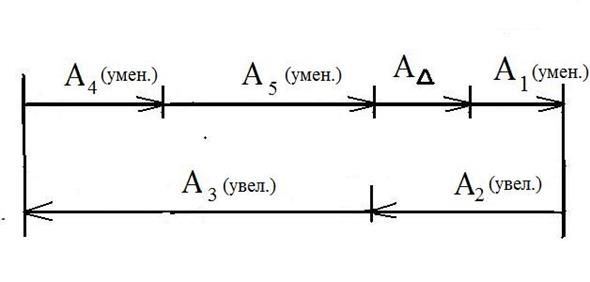
Начиная от ограничивающей поверхности замыкающего звена в произвольном направлении осуществляют обход по контуру размерной цепи и обозначают ( А₁ , А₂ и так далее).

При этом:

a)  Увеличивающими называют размеры цепи , при увеличении которых увеличивается А∆ (замыкающее звено) 

• А₂

b)  Уменьшающими называют размеры цепи, при увеличении которых уменьшается А∆

•А₃ , А₁

Примечание: В КР звенья, направленные в ту же сторону, что и А∆ являются уменьшающими, в противоположную – увеличивающими.

Расчет размерной цепи становится необходимым, если задается значение А∆.

Расчет размерных цепей.

При расчёте размерных цепей решают два вида задач - прямую и обратную.

Прямая задача (решается при проектировании) - задают номинальные размеры составляющих звеньев, номинальный размер и предельные отклонения исходного (замыкающего) звена и определяют предельные отклонения составляющих звеньев.

Обратная задача (проверка правильности прямой) - задают номинальные размеры и предельные отклонения составляющих звеньев, определяют номинальный размер и предельные отклонения замыкающего звена.

Обе задачи решаются методами:

1.  Расчёт размерных цепей методом полной взаимозаменяемости (расчёт на максимум - минимум).

2.  Расчёт размерных цепей методом неполной взаимозаменяемости.

В курсовой работе решаем прямую задачу, методом полной взаимозаменяемости, способом равной точности (способ предполагает, что все составляющие размеры выполняются с одинаковой точностью, в одном квалитете).

Пример решения в КР.

Дано А_∆ = 1 ± 0,2

Предельные размеры

А_∆max = 1,2

А_∆min = 0,8

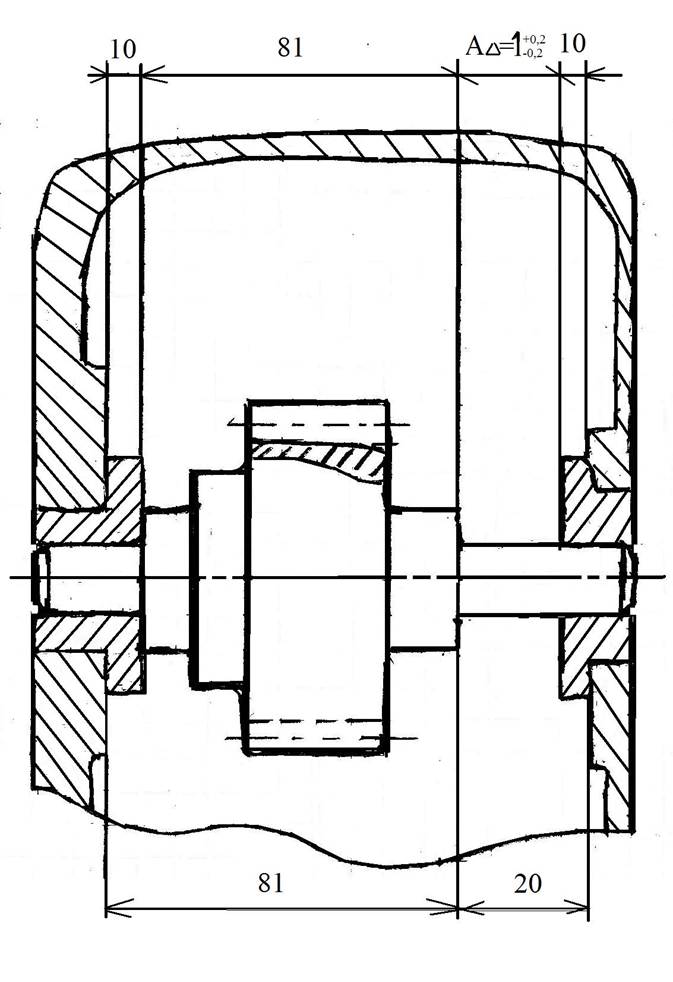
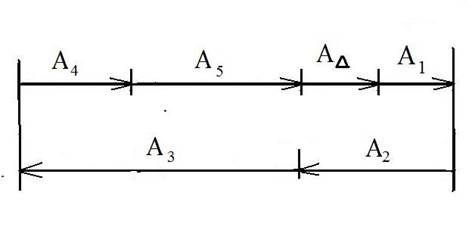
Рис. 3

А₁, А₅, А₄ – уменьшающие

А₂, А₃ – увеличивающие

Решение.

На фрагменте чертежа нанести размерную цепь (см. рис.2 , рис. 3).

Находим допуск исходного звена TA∆

TA∆ = A_∆max - A_∆min = 1,2 - 0,8 = 0,4

Находим значения единицы допуска для различных интервалов размеров (i) (см. таблицу 6.1).

Для    А₁ = 10, i = 0,9 мкм

А₂ = 20, i = 1,3 мкм

А₃ = 81, i = 2,2 мкм

А₄ = 10, i = 0,9 мкм

А₅ = 80, i = 1,9 мкм

Определяем среднее число единиц допуска a

IT = a  i, где IT – международный допуск.

Способ равной плоскости предполагает, что все составляющие размеры выполняются с одной точностью, в одном квалитете.

a = = = 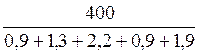55,53

Полученное значение «a» сравнивают по таблице 6.2.

Значение «a» (55,53) располагается между  9 (a = 40) и 10 (a = 64) квалитетами.

В этом случае часть размеров выполняют по более точному квалитету, а другую часть – по более грубому.

Однако, при этом условие, что все составляющие размеры выполняются в одном квалитете, не выдерживаются. Поэтому стандартные допуски назначают для всех составляющих звеньев, кроме одного, называемого увязочным.

Примечание: Принимаем за увязочный размер A₂.

Рекомендуется за увязочный размер принимать размер, контроль которого не позволяет использовать калибры.

Если при обработке деталей размер увеличивается, допуск назначают в «+», если уменьшается – в « - ».

• Вал в « - », отверстие в « + ».

Размеры A₁ , A₄ , A₅ назначаем по 9 квалитету.

Размер A₃ – по 10 квалитету.

По таблице 6.3 определяем:

A₁ = 10 h9   (-0,036)    

A₄ = 10 h9   (-0,036)

A₅ = 80 h9   (-0,074)

A₃ = 81H10 (+0,140)

Допуск увязочного звена:

TA_2увяз = TA_∆ - TA_i

               TA_2увяз = 400 – (36 + 36 + 74 + 140) = 114 мкм.

Определяем предельные отклонения A_2увяз.

 

Номинал	MAX	MIN
A1 = 10	10	9,964
A2увяз = 20
A3 = 81	81,140	81
A4 = 10	10	9,964
A5 = 80	80	79,926
A∆ = 1	1,2	0,8

Из рисунка:

A_∆max = Aув_imax - Aум_imin

A_∆max  = (A_{3max +} A_2max) – (A_4min + A_5min + A_1min )

A_2max  = - A_3max + A_∆max + A_4min + A_5min + A_1min

A_2max  = -81,14 + 1,2 + 9,964 + 79,926 + 9,964 = 19,914

A_∆min = Aув_imin - Aум_imax = (A_2min + A_3min) – (A_4max + A_5max + A_1max)

A_2min = - A_3min + A_∆min + A_4max + A_5max + A_1max

A_2min = -81 + 0,8 + 10 + 80 + 10 = 19,8

Тогда:

1.  верхнее предельное отклонение:

∆S₂ = A_2max - A₂ = 19,914 – 20 = - 0,086

2.  нижнее предельное отклонение:

∆J₂ = A_2min - A₂ = 19,8 – 20 = - 0,2

Следовательно: 20

Окончательно результаты расчета сводятся в таблицу.

Пример: см. таблицу 6.4.