Изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа

Цель работы

·  изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа;

·  освоение наиболее распространенных простейших разностных схем решения этого уравнения;

·  исследование свойств разностных схем;

·  изучение методов решения получающихся систем линейных алгебраических уравнений;

·  изучение возможных алгоритмов реализации данных методов на ЭВМ;

Исходные данные

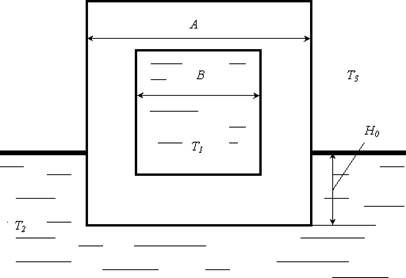
Моделируются стационарные поля температур в квадратной трубе (со стороной A), имеющей квадратное отверстие (со стороной B), по которой течет нагретая жидкость с неизменной температурой T₁. Сама труба частично опущена (на высоту H₀) в ванну с постоянной температурой T₂. Верхняя часть трубы находится при температуре T₃. См. рисунок.

Труба считается достаточно длинной, внешние условия - неизменными. Это позволяет рассматривать плоскую задачу. Распределение температур при этом удовлетворяет уравнению Лапласа (3) со следующими граничными условиями:

T(0,x)=T₂;                     T(A,x)=T₃                               при 0 ≤ x ≤ A

T(y,0)=T(y,A)=T₂                     при 0 ≤ y ≤ H₀ ;

T(y,0)=T(y,A)=T₃                     при H₀ < y ≤ A ;

A=910 - внешний размер квадратной трубы;

B=244  - размер внутреннего квадратного отверстия трубы;

H0=411 - высота, на которую труба опущена в жидкость с температурой T2;

T1=25 - температура внутренней поверхности трубы (град. C) (т.е. температура жидкости, текущей в трубе);

T2=15 - температура нижней части внешней поверхности трубы (град. C) (т.е. температура жидкости, в которую опущена труба на высоту H0);

T3=35 - температура верхней части внешней поверхности трубы (град. C).

Примечание:  все геометрические размеры приводятся в безразмерном виде.

N - количество точек разбиения расчетной области. В лабораторной работе используется квадратная сетка с одинаковыми как по оси  X  так и по оси  Y  шагами  ∆x, ∆y   по пространству, причем принимается  ;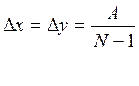

ε - критерий сходимости  ;

I_max- максимально допустимое количество итераций.

А. Для метода Рунге:

ω  -  ускоряющий множитель, использующийся в методе последовательной верхней релаксации для ускорения «основного» итерационного процесса решения системы линейных алгебраических уравнений Гаусса-Зайделя.

Б. Для методов, использующих принцип установления (простой явный, «классики», неявный метод переменных направлений, метод Н.Н. Яненко):

С - коэффициент «температуропроводности»;

∆t - шаг по времени.

NN – число шагов по времени, когда  (см. методы, использующие принцип установления).

Краткие сведения из теории

Двумерным уравнением Лапласа называется следующее дифференциальное уравнение в частных производных второго порядка эллиптического типа:

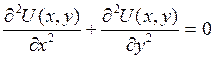
Это уравнение часто встречается в приложениях и описывает целый ряд важных физических процессов:

§  напряжения, возникающие при упругом кручении цилиндрического стержня;

§  распределение потенциалов (или электрических напряжений) на проводящей плоскости при задании потенциала на ее границе;

§  стационарные (установившиеся) поля температур в двумерном твердом теле;

§  дозвуковое (потенциальное) течение газа и т.д.

Для корректной постановки задачи необходимо задание соответствующих граничных условий. Если граничные условия задаются в виде

U(x,y)│_s = f(x,y) ,   где  S  -  граница рассматриваемой области, то задача носит название «задачи Дирихле».

В данной лабораторной работе используются методы решения модельного эллиптического уравнения Лапласа, которые условно можно разделить на два класса:

§ основанные на прямом применении той или иной конечно-разностной схемы для его решения. Получающаяся при этом система линейных алгебраических уравнений, обладающая, как правило, матрицей общего вида, решается (однократно) одним из прямых и/или итерационных методов;

§ основанные на использовании идеи метода установления, при котором решение исходной эллиптической задачи заменяется поиском решения маршевой (как правило, параболической) задачи, имеющей те же граничные условия, при    .

Краткая характеристика используемых методов

«Прямые» методы решения уравнения Лапласа

В данной лабораторной работе для решения указанного уравнения в качестве «прямого» метода предлагается использовать схему Рунге (другое название «пятиточечная схема»). Будучи примененная к уравнению Лапласа в сочетании с последующим использованием для решения получающейся системы линейных алгебраических уравнений итерационного метода Гаусса - Зайделя, она получила название «метода Либмана». Именно метод Либмана используется в данной лабораторной работе.