Изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа, страница 3

В приложении к рассматриваемому в данной лабораторной работе уравнению Лапласа принцип установления выглядит следующим образом:

необходимо найти решение уравнения Лапласа (3) с граничными условиями (4) как предел решения нестационарного двумерного уравнения «теплопроводности» параболического типа (7) с граничными условиями (8) при стремлении к бесконечности времени процесса (т.е. при ).

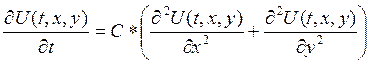                                       (7)

U(t,x,y)│ = f(x,y),                                                   (8)

│s     

C - коэффициент «температуропроводности». Причем физический смысл этот коэффициент «С» имеет лишь в случае, когда интерес представляет решение собственно уравнения теплопроводности (7). Если же (как в данной лабораторной работе) необходимо получить только стационарное решение эллиптического уравнения (3), коэффициент «С» не имеет физического смысла и выбирается из других соображение (например, для улучшения свойств применяемой конечно-разностной схемы).

Для решения параболической задачи (7) требуется (чтобы задача была корректно поставлена) знание начальных условий при t=0, т.е.

U(0,x,y)=g(x,y)                                                       (9), которые необходимо задавать точно только в случае, когда исследователя интересуют нестационарные решения собственно уравнения (7). Если же решается уравнение (3), т.е. представляет интерес только стационарное решение, то выбор начальных условий достаточно произволен. Хотя и он должен удовлетворять определенным требованиям. Естественно, чем ближе будут выбраны начальные условия g(x,y) к искомому решению эллиптического уравнения (3), тем быстрее (и с меньшими трудностями) будет получено само это решение.

Таким образом, эллиптическая задача (3, 4) сводится к решению параболической задачи (7, 8, 9). И в дальнейшем рассматриваются конечно-разностные методы решения именно параболической задачи – уравнения теплопроводности (7) с граничными условиями (8) и начальными условиями (9).

Необходимо отметить, что если исследователя интересует только стационарное решение эллиптической задачи, то ему неважна точность промежуточных решений (решений, полученных при текущем значении времени t) параболического уравнения. Важен только конечный результат, т.е. решение, полученное при  . При этом, это «установившееся» решение не будет зависеть ни от выбора коэффициента «С», ни, как отмечалось, от выбора начальных данных U(0,x,y)=g(x,y)  .

2. Простой явный метод

Для решения уравнения (7) используется простейшая явная схема.

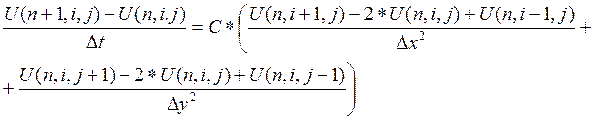
Здесь и далее U(n,i,j) – сеточное значение функции U(t,x,y)  на  n  временном слое () в пространственной точке (i,j)  -   (  ,  )

Схема одношаговая, явная, двухслойная по времени. Имеет первый порядок аппроксимации. Точнее - первый порядок точности по времени и второй - по  пространству. Таким образом, нестационарное решение имеет первый порядок аппроксимации, а стационарное (независящее от времени, установившееся) - второй. Так как нас интересует эллиптическое уравнение (3), то получаемое для него установившееся решение имеет второй порядок точности.

Схема абсолютно согласована.

Схема имеет жесткое условие устойчивости. Это условие выглядит следующим образом:

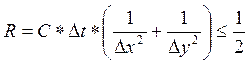  ,     причем при            ;

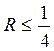Оно более жесткое (примерно в два раза), нежели в случае применения аналогичного «простого явного метода» для одномерного уравнения теплопроводности (см. лабораторную работу № 2).

Схема обладает только диссипативными ошибками. Дисперсионные ошибки отсутствуют.

Решение осуществляется маршевым методом по временной координате.

Шаги по времени можно рассматривать как отдельные итерации для нахождения решения поставленной задачи. Процесс заканчивается, когда в любой пространственной точке (i,j), полученные решения на двух соседних временных слоях (итерациях) отличаются (по абсолютной величине) на заранее заданную малую величину  ε 

  для любой точки  (i,j)  .

Точнее, поскольку промежуточное значение искомых переменных может по-разному себя вести по мере установления (при ), то для окончательного принятия решения об окончании указанного итерационного процесса необходимо убедиться, что, кроме приведенного выше, выполняется еще и следующее неравенство   для любой точки  (i,j)  ,  где  NN – достаточно большое число. Это, например, важно, когда промежуточные решения совершают в процессе установления колебания вокруг искомого «стационарного» решения.

Примерная картина изолиний (при ε=0.2)

При R=0.145 (1553)          При R=0.322

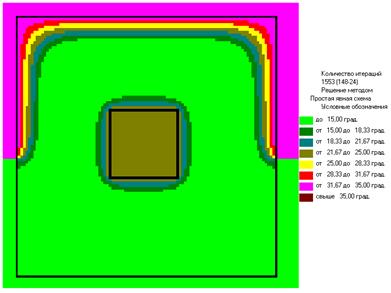
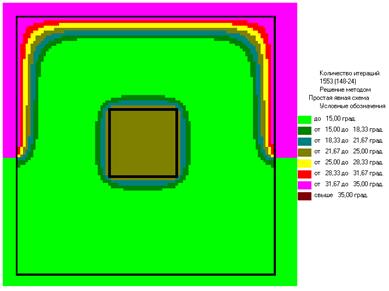
При R=0.5                   При R=1.920

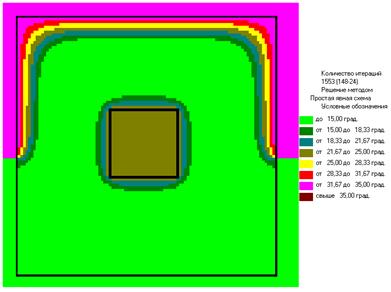
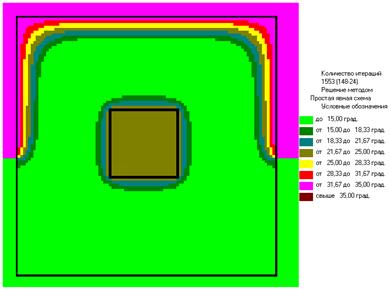
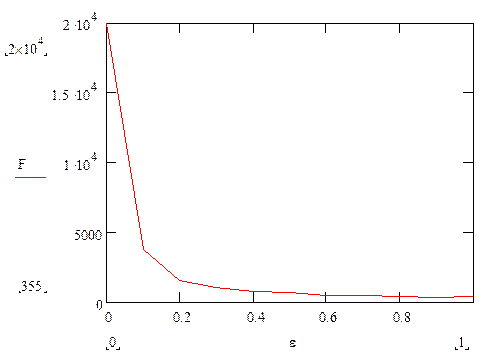
Влияние числа 'ε' (0< ε <1) на количество итераций. График  Iter=F(ε). При R=0.5