Изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа, страница 2

1. Схема Рунге (пятиточечная схема)

Простейшая пятиточечная схема выглядит следующим образом:

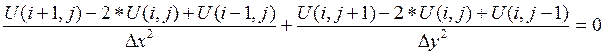       (5)

Модифицированное уравнение (дифференциальное приближение) этой схемы имеет следующий вид:

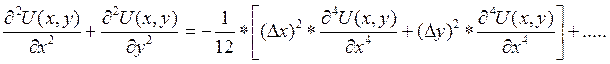
Схема имеет второй порядок аппроксимации. Абсолютно согласована. Превалируют диссипативные ошибки.

При  ∆x=∆y  разностные уравнения имеют вид:

                           (6)

Уравнение (5) или (как в данной лабораторной работе) уравнение (6) записывается для всех узлов сетки, в которых величина U(i,j) неизвестна, т.е. для всех ее «внутренних» узлов. Если задача решается в квадрате, каждая сторона которого разбита  N  точками на (N-1) отрезков, то (при граничных условиях Дирихле) в каждом из внутренних узлов должно удовлетворяться разностное уравнение (5) или (6). При этом необходимо одновременно решать (N-2)*(N-2)  линейных алгебраических уравнений с  (N-2)*(N-2)  неизвестными.

Данные системы алгебраических уравнений решаются различными методами, которые условно можно разделить на две группы:

а.) прямые (правило Крамера; метод исключения Гаусса и т.д.);

б.) итерационные (метод простой итерации. метод Гаусса-Зайделя; метод последовательной верхней релаксации; блочные итерационные методы и т.д.).

В данной лабораторной работе используется итерационный метод Гаусса-Зайделя, который при применении к уравнению Лапласа часто, как уже отмечалось, называют методом Либмана (ω=1). Для ускорения сходимости данного итерационного процесса используется метод последовательной верхней релаксации с ускоряющим множителем ω, причем    . При ω=1 реализуется сам метод Гаусса-Зайделя без ускорения, а при    -   метод последовательной нижней релаксации, замедляющий процесс сходимости.

Основные этапы реализации этого метода определяются следующим  образом:

1. задается начальное приближение (при этом, значение одной из неизвестных можно не задавать);

2. перестановкой строк и/или столбцов располагают на главной диагонали матрицы этой системы линейных алгебраических уравнений, по возможности, наибольшие коэффициенты. Это связано с тем, что метод Гаусса-Зайделя не всегда сходится. Достаточным (но не необходимым) условием сходимости этого метода является выполнение следующих неравенств:

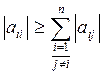  для всех  i  и, кроме того, хотя бы для одного  i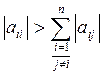  

где  a_ij  -  коэффициенты указанной матрицы.

Поэтому, чтобы расширить диапазон сходимости применяемого метода, и располагают на главной диагонали матрицы как можно большие коэффициенты;

3. из каждого уравнения определяют одну неизвестную, коэффициент перед которой имеет наибольшую абсолютную величину, при этом используются заданные начальные значения и уже вычисленные значения других неизвестных;

4. процесс решения уравнений повторяется итерационно до тех пор, пока значения неизвестных на двух последовательных итерациях не будут отличаться на достаточно малую наперед заданную величину 'ε'. При этом надо в правую часть каждого уравнения подставлять уже вычисленные значения неизвестных.

Как отмечалось, в данной лабораторной работе используется также метод  последовательной верхней релаксации с ускоряющим множителем ω, причем 1< ω <2. Этот метод может быть использован для ускорения любого  итерационного процесса (в данной лабораторной работе - метода  Гаусса-Зайделя). Идея его состоит в коррекции неизвестных на  очередном шаге итерации

   ,   где

  -  скорректированное значение неизвестной на новом  (n+1)  шаге итерации;

  -  значение неизвестной на последнем  (n+1)  шаге итерации (без коррекции);

  -  значение неизвестной на предыдущем  n  шаге итерации.

График зависимости количества итераций от величины ускоряющего множителя  'ω'  -   Iter=F(ω)

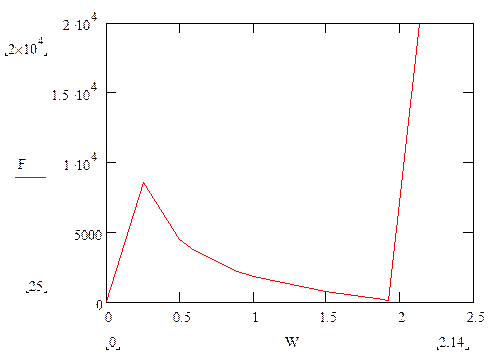
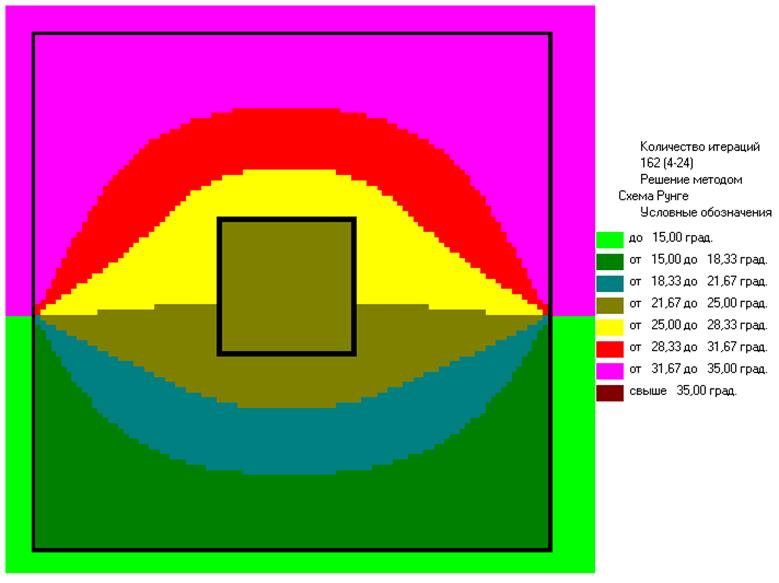
оптимальное значение ускоряющего множителя ωопт = 1.91, примерная картина изолиний при нем (при ε=0.1)

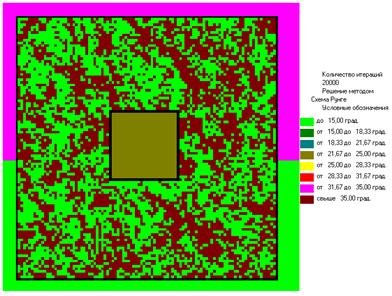
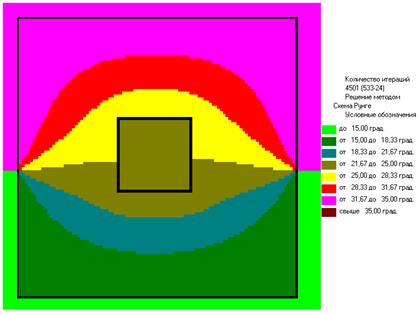
при ω=0.5                                                     приω=2.14

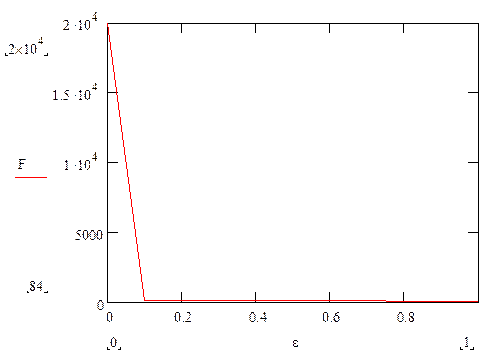
Влияние числа 'ε' (0< ε <1) на количество итераций. График  Iter=F(ε). При ωопт = 1.91.

Методы решения уравнения Лапласа, использующие идею принципа установления

В данной лабораторной работе предлагается использовать для решения эллиптического уравнения Лапласа конечно-разностные методы, основанные на принципе установления.

Принцип установления заключается в том, что стационарное решение эллиптической задачи находится как предел нестационарного решения соответствующей маршевой задачи при стремлении к бесконечности времени процесса (т.е. при   ). Естественно, что все граничные условия новой маршевой задачи должны быть стационарными (т.е. не зависящими от времени) и такими же, что и у исходной эллиптической.