Вопросы и примеры задач к зачёту по курсу "Вычислительная математика"

Группы ВИ306, ВИ307

Преподаватель В.Г. Пак

Часть I. Элементарная теория погрешностей

1.  Источники и классификация погрешностей. Абсолютные и относительные погрешности. Верные значащие цифры. Округление

2.  Погрешности арифметических  операций

3.  Погрешность вычисления функции

Часть II. Вычислительные задачи и методы

1.  Корректность и обусловленность вычислительной задачи

2.  Классификация вычислительных методов

Часть III. Аналитическое приближение табличных функций

1.  Постановка задачи приближённого вычисления функции. Задача интерполяции. Полиномиальная интерполяция, её погрешность

2.  Интерполяционный многочлен Лагранжа

3.  Разделённые разности, их свойства. Интерполяционные многочлены Ньютона с разделёнными разностями

4.  Конечные разности, их свойства. Интерполяционные многочлены Ньютона с конечными разностями

5.  Вычислительная схема Эйткена

6.  Постановка задачи аппроксимации табличной функции. Аппроксимация обобщёнными многочленами методом наименьших квадратов

7.  Полиномиальная аппроксимация методом наименьших квадратов

Часть III. Численное дифференцирование

1.  Постановка задачи численного дифференцирования. Разностные формулы численного дифференцирования для первой производной

2.  Погрешности разностных формул численного дифференцирования для первой производной

3.  Формула второй центральной разностной производной, её погрешность

4.  Влияние погрешностей табличных данных на погрешности разностных формул численного дифференцирования

Часть IV. Численное интегрирование

1.  Постановка задачи численного интегрирования. Простейшие квадратурные формулы

2.  Формулы левых и правых прямоугольников, их погрешность

3.  Формула центральных прямоугольников, её погрешность

4.  Формулы трапеций и парабол, их погрешности

Часть IV. Численное решение задачи Коши

1.  Задача Коши для обыкновенного дифференциального уравнения первого порядка. Дискретизация задачи

2.  Метод Эйлера

3.  Модификации метода Эйлера

Примеры задач

1. Оценить абсолютную и относительную погрешности значения функции, округлить его до верных цифр:

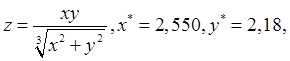      аргументы даны с верными знаками.

2.   Оценить абсолютную и относительную погрешности результата, округлить его до верных цифр:

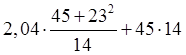, все значения даны с верными цифрами.

3.   Оценить абсолютную и относительную погрешности значения функции, округлить его до верных цифр:

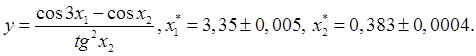        Константа 3 точная.

4.   Оценить абсолютную и относительную погрешности результата, округлить его до верных цифр:

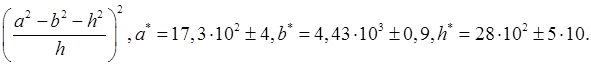
5.  Построить интерполяционный многочлен Лагранжа для данной таблицы:

6.  Построить интерполяционные многочлены Ньютона с конечными разностями 1-го и 2-го типов для данной таблицы:

7.   Построить интерполяционные многочлены Ньютона с разделёнными разностями 1-го и 2-го типов для данной таблицы:

8.   Аппроксимировать данную табличную функцию многочленами 1-й и 2-й степени. Вычислить наилучшие среднеквадратические отклонения.

9.   Вычислить интеграл от функции y(x)=  по отрезку [1;5] с разбиением на 5 частичных отрезков с помощью формул прямоугольников, трапеций, парабол. Оценить абсолютные погрешности формул прямоугольников и трапеций. Округлить результаты до верных знаков.

10. Решить методом Эйлера (Эйлера-Коши, серединных точек) задачу Коши

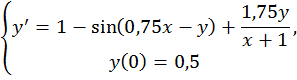
на отрезке  с шагом сетки .