




Gcz|=Icz|ωz|=
Icz|![]() ; Wcx=
; Wcx=![]() ; Wcy=
; Wcy=![]()
![]() m
m![]() =
=![]() jxe
jxe
m![]() =
=![]() jye
(56) дифф-е
уравнения пл.-пар.
jye
(56) дифф-е
уравнения пл.-пар.
Icz|![]() =
=![]() |(Fje)=Lecz|
движения а.т.т.
|(Fje)=Lecz|
движения а.т.т.
Для определения неизвестных необходимо задать 6 н. усл.
При t=t0=0 ; xc=xc0 , yc=yc0 , Φ=Φ0 ;
(![]() )0=vc0x ; (
)0=vc0x ; (![]() )0=vc0y ; ; (
)0=vc0y ; ; (![]() )0=ω0z| .
)0=ω0z| .
Дифф-е уравнения вращения а.т.т. вокруг неподвижного полюса (уравнение Эйлера).
(см. ниже!)
Общий случай движения а.т.т. (свободное движение)
(см. ниже!)
Динамика несвободной точки и системы материальных точек.
Определение: Движение вещественной точки называется несвободным , еслионо ограничено какими-либо телами (ограничениями, связями); такую точку называют несвободной.
Определение: Тела, препятствующие перемещению вещественной точкив каком-либо направлении, называются ограничивающими (ограничениями).
Определение: Силы, характеризующие механическое действие на данную точку со стороны ограниченного тела, называются силами реакции ограниченного тела.
Связи, которым подчинено движение точки, можно записать в виде аналитических зависимостей, которые содержат время, координаты и скорости (производные от координат).
В зависимости от вида аналитической записи ограничения (связи); их можно классифицировать по 3 основным типам:
1.Удерживающие (двухсторонние) и неудерживающие (односторонние) ограничения;
2.Изменяемые (нестационарные) и неизменяемые (стационарные);
3.Конечные (голономные) и дифференциальные (неголономные).
Определение: Удерживающими (двухсторонними) ограничениями называются ограничения, которые веществ. точку не может покинуть во всё время движения.
Аналитическая запись: f(t,x,y,z,![]() ,
,![]() ,
,![]() )=0 (1)
)=0 (1)
Определение: Неудерживающими (односторонними) называются ограничения, которые веществ. точку в некоторый момент времени может покинуть
Аналитическая запись: f(t,x,y,z,![]() ,
,![]() ,
,![]() )≷0 (2)
)≷0 (2)
Определение: Изменяемыми ограничениями называются ограничения, в аналитическую запись которых явно входит время t:
f (t, x, y, z,![]() ,
,![]() ,
,![]() )=0 (3)
)=0 (3)
Определение: Неизменяемыми ограничениями называются ограничения, в аналитическую запись которых время t явно не входит.
f ( x, y, z,![]() ,
,![]() ,
,![]() )=0 (4)
)=0 (4)
Определение: Ограничения, в аналитическую запись которых не входят производные от координат (скорости) точки, называются конечными (голономными).
f (t, x, y, z)=0 (5)
Определение: Если в аналитическую запись ограничения входит производная от координат точки, то такое ограничение называется дифференциальным (неголономным).
Пример: OM- невесомый стержень
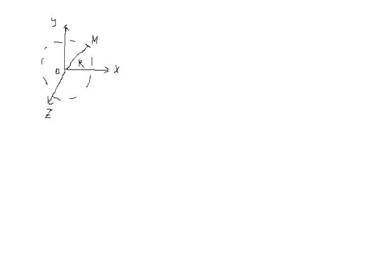 x2+y2+z2=R2
x2+y2+z2=R2
Огр: удерж., неизмен.,конечное
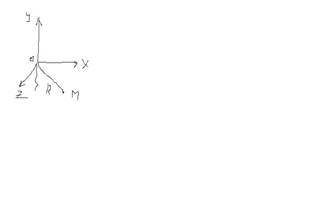 OM-нить
OM-нить
x2+y2+z2≤R2
Классификация сил, действующих на несвободную вещественную точку.
Определение: Силы, действующие на невесомую вещественную точку можно подразделить на два вида: 1. Силы, не зависящие от ограничений 2. Силы, зависящие от ограничений.
![]() =
=![]() +
+![]()
![]() - равнодействующая всех сил, не зависящих от ограничений (активных)
- равнодействующая всех сил, не зависящих от ограничений (активных)
![]() - равнодействующая всех сил, зависящих от ограничений (сил реакций).
- равнодействующая всех сил, зависящих от ограничений (сил реакций).
m![]() =
=![]() +
+![]() (57) – основное уравнение динамики несвободной
вещественной точки.
(57) – основное уравнение динамики несвободной
вещественной точки.
Динамика несвободной системы вещественных точек.
Определение: Система вещественной точки называется несвободной, если хотя бы одна точка этой системы несвободна.
Ограничения, наложенные на систему вещественных точек, будут классифицироваться так же, как в динамике точки.
f2(t,x,y,z,…,xn,yn,zn,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() )≤0
)≤0
неуд., изменяемое, дифференц. (r=1,2,…,h)
Определение: Систему вещественных точек, на которую наложены (подчиняется) только конечным ограничениям, будем называть голономной.
Пусть система вещественных точек, состоящая из «n» точек массами (m1,m2,…,mn) двигаются относительно осей координат OXYZ под действием системы сил.
![]() ,
,![]() ,…,
,…,![]() } положение точки будет определяться 3 координатами.
} положение точки будет определяться 3 координатами.
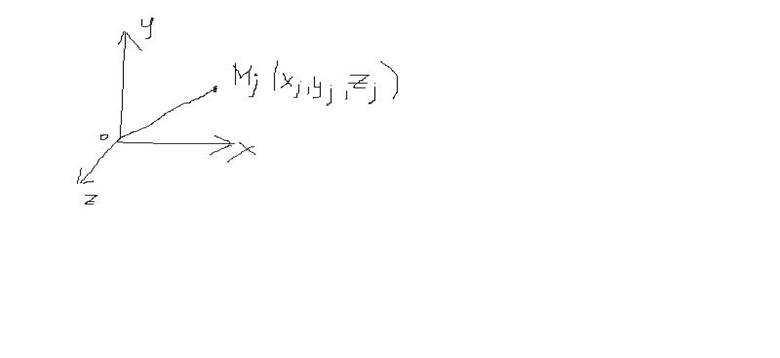
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.