Способы обнаружения ошибок в комбинациях линейных блоковых кодов, страница 3

Последние r столбцов – единичная матрица размера . Таким образом матрица Н состоит из двух подматриц:

       (8)

из структуры матриц G и H следует, что между ними существует тесная связь, если известна одна из этих матриц, то по ней всегда может быть получена другая.

Пример:

Построить матрицу Н линейного (7,4)-кода, задаваемого первым набором коэффициентов С_ji.

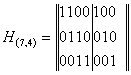
Удобство матрицы Н состоит в том, что, используя ее, легко получить синдром принятой комбинации. Действительно каждый элемент синдрома s_j в соответствии с формулой (6) находится как скалярное произведение прямой комбинации V^* и j-той строки матрицы Н.

Учитывая правило умножения матриц можно записать, что синдром:

    (9)

Если V^* является комбинацией линейного кода, то все элементы синдрома равны нулю, поэтому (матрицу строку из одних нулей)

                                              (10)

 Найдем синдром комбинации 0001001 линейного (7,4)-кода, полученной из комбинации 010101

    

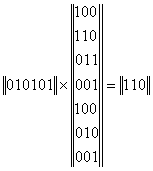
получим тот же синдром, что и при использовании ТЛФ.

Отличие синдрома от нуля свидетельствует о наличии в прямой комбинации ошибок.

Найдем теперь от чего зависит вид комбинации синдрома. Запишем принятую комбинацию синдрома .

Найдем синдром принятой комбинации, воспользовавшись формулой (9):

  (11)

Из формулы (11) видно, что синдром принятой комбинации не зависит от передаваемой комбинации линейного кода, а определяется только исказившим ее вектором ошибок.

§Второе определение циклического кода. Порождающий многочлен циклического кода.