Задание движения твердого тела. Поступательное движение твердого тела. Вращение твердого тела вокруг неподвижной оси

Задание движения твердого тела

При движении твердого тела отдельные его точки движущиеся в общем случае по различным траекториям и имеют в каждый момент времени различные скорости и ускорения.

Основные задачи кинематики твердого тела – установление способа задания его движения, излучение кинематических характеристик, присущих твердому телу и определение траекторий, скоростей и ускорений всех точек тела.

Покажем, что положение твердого тела в общем случае определяется заданием 6 независимых параметров. Возьмем в теле 3, не лежащие на одной прямой, точки М₁, М₂, М₃ с координатами

M₁(*)x_к = x_к(t), y_к=y_к(t), z_к=z_к(t)     к = 1,2,3

Так как расстояния  d₁₂, d₂₃, d₁₃  между точками твердого тела не изменяются, то  координатами точек должны удовлетворять трем уравнениям

d₁₂²=(x₁-x₂)²+(y₁-y₂)²+(z₁-z₂)²,

d₁₃²=(x₁-x₃)²+(y₁-y₃)²+(z₁-z₃)²,               (**)

d₂₃²=(x₂-x₃)²+(y₂-y₃)²+(z₂-z₃)².

Следователь, из 9 координат (*) независимых только 6. Если взять еще одну (.) М₄ с координатами x₄, y₄, z₄, то эти координаты должны удовлетворять 3 уравнениям вида (**). Таким образом, положение твердого тела относительно произвольно выбранной системы координат определяется 6 независимыми параметрами.

Число независимых параметров, задание которых однозначно определяет положение твердого тела в пространстве, называется  числом степеней свободы твердого тела.

Задание 6  декартовых координат не является наилучшим способом задания движения твердого тела.

Поступательное движение твердого тела

Движение тела, при котором прямая, соединяющая две любые точки этого тела, перемещается, оставаясь параллельной своему начальному направлению.

Спарка ОАВО’ – все время остается  параллельна.

Точки твердого тела могут двигаться по любым траекториям

Oxyz- неподвижная система координат      Px’y’z’ жестко связана с телом.

Оси  //  осям Oxyz. Положение  системы Px’y’z’  определяют уравнения

x_p = x_p(t),

y_p = y_p(t),

z_p = z_p(t), а следовательно и положение твердого тела

Твердое тело при поступательном движении имеет 3 степени свободы.

(.)М – произвольная.  В любой момент времени:

 - постоянна по величине и по направлению.

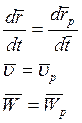
При поступательном движении  твердого тела  точки тела описывают одинаковые траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.

Вращение твердого тела  вокруг неподвижной оси

Движение тела, при котором все точки, лежащие на некоторой прямой, неизменно связанной с телом, остаются неподвижными в рассматриваемой системе отсчета.

Возьмем на оси вращения две точки А и В и введем систему координат  Ax₁y₁z₁. Так как положение точек А и В известно, то  положение  твердого тела будет  полностью определено, если известно положение (.) с (не лежащей на оси вращения) в любой момент времени. Из трех координат (.) С независима одна, т.к. АС и ВС -  const  и  координаты точки связаны уравнениями:

(x_A – x_C)² + (y_A – y_C)² + (z_A – z_C)² = AC²

(x_B – x_C)² + (y_B – y_C)² + (z_B – z_C)² = BC²

Таким образом, положение  твердого тела, вращающегося вокруг неподвижной оси, определяется одним параметром.

Направим ось  Az₁  неподвижной системы координат Ax₁y₁z₁ по оси вращения  твердого тела Axyz  - подвижная система координат, жестко связанная с телом. Положение  твердого тела определено, если задан угол   φ = φ(t)  между плоскостями    x₁Az₁  и xAz     - угол поворота тела.

Положительное направление отсчета   φ  - против хода часовой стрелки, если смотреть с  конца оси  Az₁.

Пусть в момент времени  t  угол между  x₁Az₁  и xAz   равен  φ(t), а в момент