|
Amin = |
(1.3) |
Подставляя численное значение в выражение (1.2) получаем
|
σmax = |
(1.4) |
Найдем σmin по формуле
|
σmin = |
(1.5) |
Определим коэффициент ассиметрии цикла
|
R
= |
(1.6) |
В качестве предельных напряжений σпр следует выбрать предел ограниченной выносливости для детали σRдN , который может быть найдет по формуле [1, c.33]
|
σRдN = |
(1.7) |
где σRдN – предел ограниченной выносливости детали при произвольном цикле, Н/мм2 ; σ-1дN предел при ограниченной выносливости для детали при произвольном цикле, Н/мм2 ; ψσд – коэффициент чувствительности детали к ассиметрии цикла; σт – предел текучести при растяжении, Н/мм2.
Определим предел ограниченной усталости для детали при симметричном цикле σ-1дN по формуле [1, c.30]
|
σ1дN = |
(1.8) |
где σ-1д – предел длительной выносливости для детали, Н/мм2 , который определяется как [1, c.20]
|
σ1д = |
(1.9) |
Учитывая, что материал легированная сталь и зная, что σВ = 670 Н/мм2 [1, с.74] найдем предел выносливости гладкого стандартного образца σ-1 [1, с.77]
|
σ1 =0,4 , σ1д =0,4∙670=268 Н/мм2 |
(1.10) |
Коэффициент чувствительности детали к ассиметрии цикла ψσд будет равен [1, с.31]
|
Ψσд = |
(1.11) |
где
ψσ =0,02+2∙10-4 ∙ σВ = 0,02+2∙10-4∙670=0.154
Определим значение коэффициента снижения предела выносливости К, учитывающего влияние различных факторов по формуле [1, с.21]
|
К= |
(1.12) |
где Кσ – коэффициент концентрации напряжений; Кdσ – масштабный фактор; КFσ – коэффициент, учитывающий шероховатость поверхностей; КV – коэффициент влияния поверхностного упрочнения; КА – коэффициент анизотропии.
Так как в данном случае деталью является шток, то заготовка представляет собой прокат, т.е. КА = 1 [1, с.29]. Считая, что дополнительная обработка поверхтности не производилась, принимаем КV =1 [1, с.28].
Определим Кσ по формуле [1, с.22]
|
Кσ = 1+q(ασ -1) |
(1.13) |
где q – коэффициент чувствительности металла к концентрации напряжений; ασ – теоретический коэффициент концентрации напряжений.
Найдем ασ по графику [1, с.78]. Учитывая, что D/d=1,3 и r/d=0,11, получаем ασ = 1,75.
При σТ / σВ = 500/670 = 0,75 [1, с.74] коэффициент q определяется по графику [1, с.84] и равняется q=0,9.
Подставляя полученные значения в выражение (1.13), получаем
Кσ = 1+0,9(1,751)=1.68
Коэффициент Кdσ в данном случае будет равен Кdσ = 0,87, а КFσ = 0,72 [1, c.85].
Подставим численные значения в формулу (1.12) и вычислим К
К=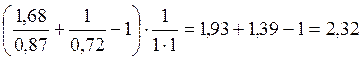
Определим К0 [1, c.30]
|
К0 = |
(1.16) |
где NG – базовое число циклов напряжений, соответствующее точке перелома кривой усталости; N – число циклов.
NG принимаем равное NG = 2·106 циклов [1, c.30].
Найдем m, показатель степени кривой усталости, по формуле [1, c.30]
|
m
= |
(1.17) |
так как ![]() , то
, то
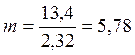
Подставляя значения в выражение (1.14), получаем
К0 =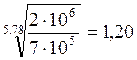
Возвращаясь к формулам (1.8) и (1.10), найдем численные значения σ-1д и ψσд
σ-1д =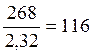 Н/мм2 и ψσд =
Н/мм2 и ψσд =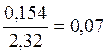
σ-1дN будет равняться
σ-1дN =116∙1,20=139 Н/мм2
Подставляя численные выражения в выражение (1.6) получаем
σRдN =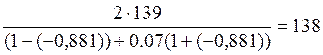 Н/мм2
Н/мм2
Сравним полученный результат со значением σТ . σRдN =138 Н/мм2 , σТ =500 Н/мм2 . следовательно σRдN меньше. В качестве предельно допустимого выбираем меньшее, то есть σRдN .
Таким образом, делаем вывод о том, что разрушение будет происходить из-за усталости.
Проверим условие прочности для данного штока
S≥[S]
Вычислим S по формуле (1.1) , принимая σпр = σRдN , получаем
S=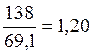
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.