Структурный и кинематический анализ плоского позиционного кулачковаго механизма (число подвижных звеньев - 2)

Балтийский Государственный Технический Университет

им. Д.Ф. Устинова «ВОЕНМЕХ»

 

Лабораторная работа  № 2 по курсу ТММ

Структурный и кинематический анализ кулачковаго механизма

Вариант 6 - 8

Преподаватель: Лавров В.Ю.

                                                                           Студент:    Туркин А.И.

                                                                     Группа:    М-231

Санкт – Петербург

2005 год

1. Структурный анализ механизма

Исследуется плоский позиционный кулачковый механизма с толкателем, силовым замыканием, с роликовым контактом, структурная схема которого представлена на рис.1, где 1- кулачёк, 2 – толкатель, 3 – ролик, Р – рабочий профиль, Ц – центровой профиль, R0 – радиус базовой окружности, е – эксцентриситет, γ – угол давления.

Число степиней свободы механизма:

W=3n - 2p₅ – p₄ = 3 *2 – 2 * 2 – 1 = 1, где n – число подвижных звеньев, p_k.– количество кинематических пар k – ого класса.

При вычислении числа степеней свободы ролик как пассивное звено и кинематические пары, им образуемые,  не учитываются.

Механизм имеет четыре фазы работы: удаление, дальний выстой, возврат и ближний выстой. Соответствующие конструктивные углы кулочка, β_У, β_Д, β_В, β_Б, обозначены на рис. 1.

На рисунке показан угол давления γ, измеряемый между вектором реакции R со стороны кулачка на толкатель и вектором скорости толкателя V_T.

2. Кинематический анализ механизма

Кинематический анализ производится эксперементально-теоретически с использованим разложения в ряд Фурье. Функцию положения F(φ) толкателя 2 в зависимости от угла поворота кулачка 1 получаем экспериментально.

Полагая, что кулачек вращается равномерно с угловой скоростью ω = 50 1/с, получаем функцию положения толкателя от времени F(t), разлагаем её в ряд Фурье и дифферинцированем ряда определяем зависимости скорости V(t) и ускорения A(t) толкателя. При этом необходимо решить вопрос о достаточном числе членов ряда.

Разложение функции в ряд Фурье означает ее приближенную замену тригонометрическим полиномом вида.

      

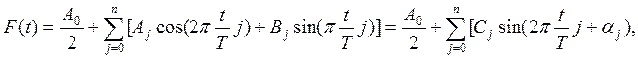
где T=2π,   ω=2π*50=0,12566 с – время полного оборота кривошипа,  - амплитуда сигнала на j-й частоте.

Частота сигнала для j-й гармоники   T

Поскольку в данном случае функция F(t) заданна таблицей значений в конечном числе точек m, то максимальное число членов ряда n(max)=m/2/

Формулы для вычисления коэффициентов ряда Фурье при табличном значении функции:

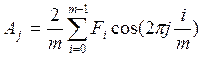
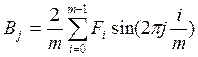              , где Fi – значение функции F(ti),i-0,1,2,…m-1.

В таблице № 1 представлена эксперементальная зависимость функции перемещения толкателя F(φ) с шагом Δφ = 10˚ по углу поворота кулачка.

Таблица  1

φ	0	0.175	0.35	0.525	0.7	0.875	1.05	1.225	1.4	1.575	1.75	1.925
s	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5

2.1	2.275	2.45	2.625	2.8	2.975	3.14	3.325	3.5	3.675	3.85	4.025	4.2
2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,3	2,0	1,1	1

4.375	4.55	4.725	4.9	5.075	5.25	5.425	5.6	5.775	5.95	6.125	6.3
0,4	0,1	0	0,4	0,7	1,2	1,7	2,3	2,5	2,5	2,5	2,5

Шаг по времени при этом: Δt= Δφ / ω= 10 * 3,14 / (50 * 180)= 0,00349 с.

Обработку данных эксперимента проведём с помощью программы FOURIER.

На первом этапе разложим F(t) в ряд с максимално возможным числом членов: s = n_max = m / 2= 36 / 2 = 18 (рис. 2). В этом случае значени ряда Фурье в узлах практически совпадают с данными эксперимента.

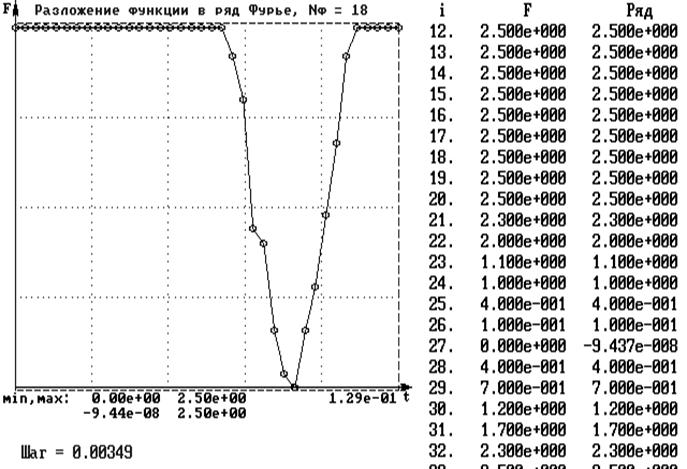
Рис.2

Результат дифференцирования ряда по времени представлении на рис. 3. На графике скорости V(t) и особенно ускорения A(t) явно видны паразитные осцилляции, вызванные погрешностями замера значений F(t). Возникает необходимость сглаживания этих зависимостей. Кроме того, на графике скорости и особенно ускорения неудовлетворительно аппроксимированы участки фаз выстоя.

Анализ амплитудного спектра  функции  (рис.4) показывает, что существенными, кроме A0/2, являются лишь слагаемые ряда Фурье, соответствующие 1 – 5 –й частотам, однако исследования показали, что наилучшие результаты достигаются при 5 членах ряда. На рис.5 показаны результаты такой аппроксимации.  На рис.6 представлены результаты двукратного дифференцирования ряда в этом случае.

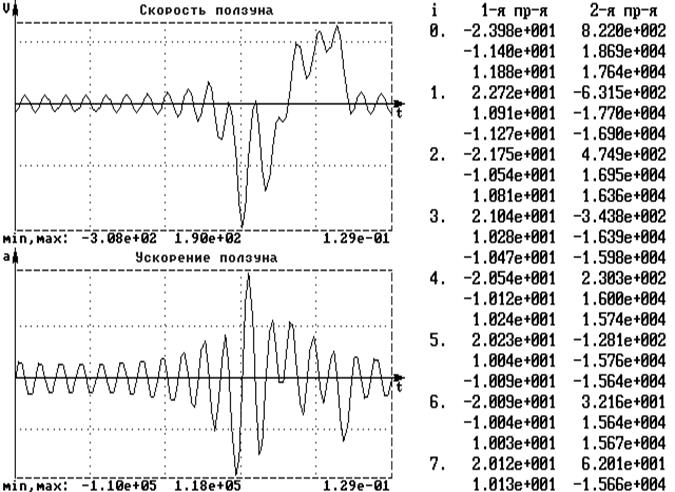
Рис.3

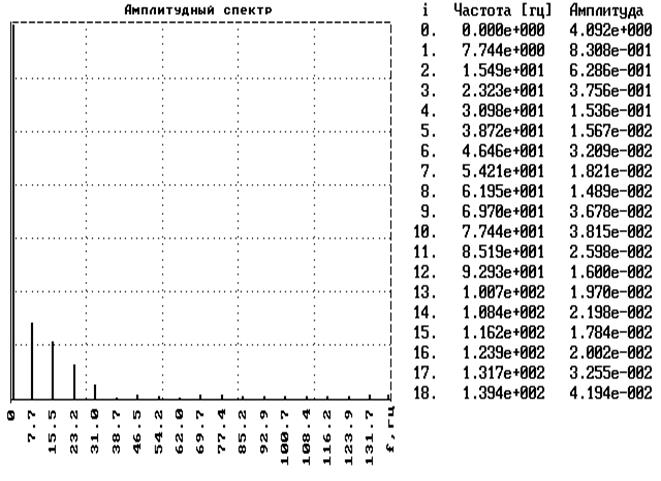
Рис.4

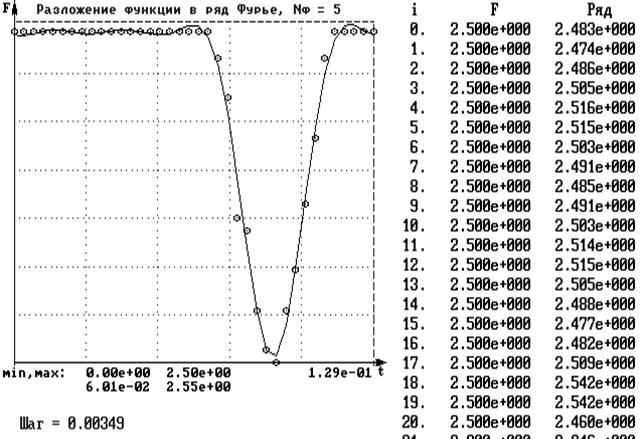
Рис.5

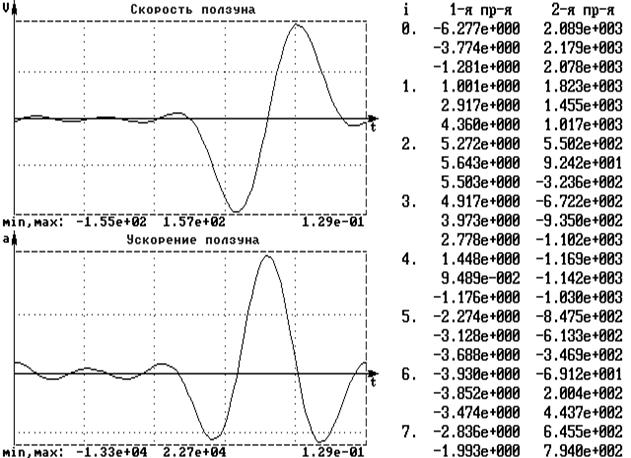
Рис.6

Анализ представленных зависимостей показывает, что удалось несколько сгладить погрешности эксперимента. Функция удовлетворительно аппроксимирована на всем участке. На фазах удаления и возврата также удовлетворительно аппроксимированы и производные, особенно скорость. Однако аппроксимировать производные на фазах выстоя удовлетворительно не удалось, особенно это касается ускорения.

Выводы по работе:

1.  Ряд Фурье хорошо аппроксимирует лишь достаточно гладкие функции.

2.  В данном случаи функция аппроксимирована удовлетворительно во всем диапазоне.

3.  Производные аппроксимированы удовлетворительно на фазах удаления и возврата во всех точках этих фаз, кроме крайних. На краях фаз удаления и возврата имеются заметные погрешности, особенно для ускорения.

4.  на фазах выстоя производные, особенно ускорение, аппроксимированы с большими погрешностями.

5.  Если функция состоит из разнородных участков, о целесообразно аппроксимировать каждый участок в отдельности.