Метод планов
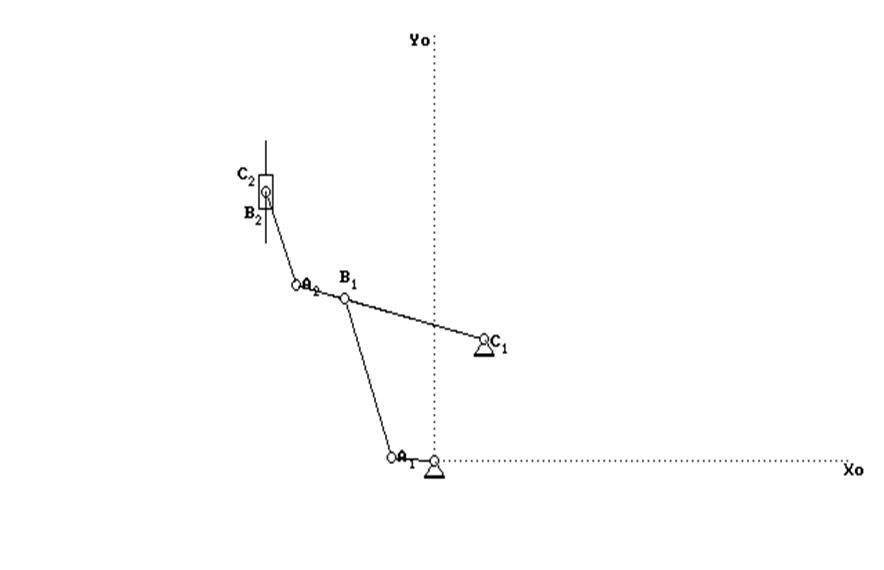
Дано: ОА1 = 0,07; А1В1 = 0,21; В1С1 = 0,23; С1А2 = 0,2875; А2В2 = 0,12
φ1 = 60°, ω1 = 10,472 рад/с, ε1 = 0
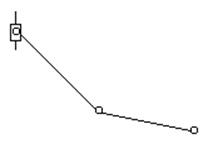
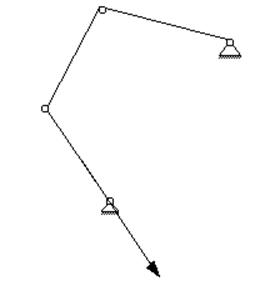
Разобьем главный механизм на составляющие простые механизмы
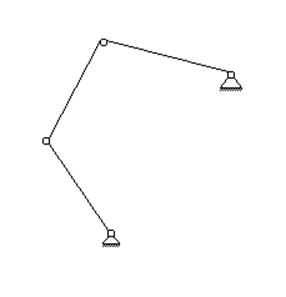
и
Метод скоростей
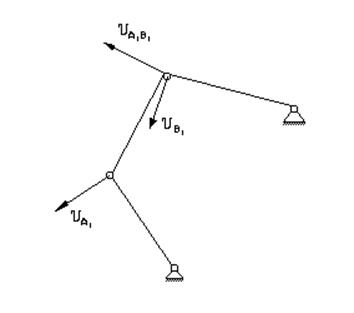Рассмотрим первую схему
1) Вычислим скорость точки А
υА1 = ω1Lкр = 5,23 * 0,125 = 0,654 м/с
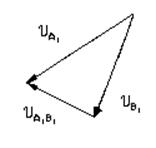
2) Запишем систему векторных уравнений для точки В
υВ1 = υА1 + υВ1А1
υВ1 = υС1 + υВ1С1
где υС1 = 0 – Скорость тачки С
Система уравнений решается графически. Проводя линию действия υВ1С1 перпендикулярно А1В1 и линию действия υВ1 = υВ1С1 перпендикулярно В1С1.
Пересечение Этих прямых и будет искомым решением.
Теперь рассмотрим вторую
схему
υА2 = υВ1
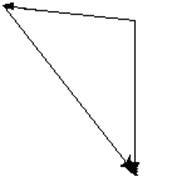
Запишем систему векторных уравнений для точки В2 вектор υВ2 колланиалин оси Y0.
υb2 = υa2 + υb2a2
где: υb2a2 – скорость точки В2 относительно точки А2
Система уравнений решается графически, проводя линию действия υb2a2 перпендикулярно А2В2 и линию действия υb2 параллельно оси Yo.
Метод Ускорений
Рассмотрим первую схему
Вычислим ускорение точки А1
Так
как ε1 = 0, то получим
Аа1 = Аna1 = ω12Lпр = 7,68
Запишем систему векторных уравнений для точки В1.
Ab1 = Aa1 + Ab1a1n + Ab1a1 τ
Ab1 = Ac1 + Ab1c1n + Ab1c1 τ
где: Ас1 = 0 – ускорение точки С1
Нормальные составляющие
Ab1a1n = υВ1А1 2 /А1В1
Ab1c1n = υВ1С1 2 /В1С1
Проводим линии действия касательных составляющих ускорения. Пересечение этих линий даёт искомое решение
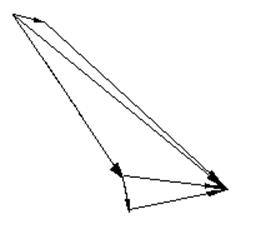
Теперь рассмотрим вторую схему
АА1 = АВ1
запишем систему векторных уравнений для точки В2
АВ2 = АА2 + АВ2А2n + AB2A2τ
Нормальная составляющая: АВ2А2n = υb2a2 / АВ, параллелен шатуну, от точки В2 к точке А2. Проводим линию действия касательной состоящей относительного ускорения.
 |
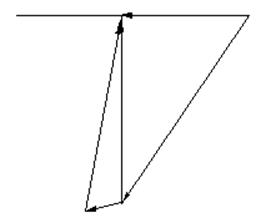Пересечение линий даёт искомое решение.
Метод векторных контуров
Разобьём главный механизм на составляющие, так же как и в методе планов.
Рассмотрим первую схему
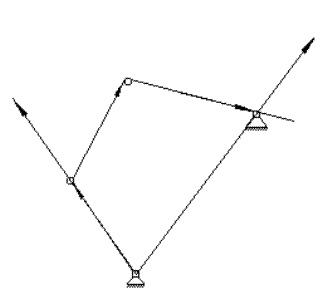
Звенья механизмов представляют в виде векторов Li. Механизм замкнут, уравнение замкнутости векторного контура:
L1 + L2 + L3 + L4 = 0 (1)
Проецируя на неподвижной системы координат OX0Y0 получим систему уравнений для определения φ 2, φ3:
L1cos φ1 + L2 cos φ2 + L3 cos φ3 + L4 = 0
L1sin φ1 +L2 sin φ2 +L3 sin φ3 = 0 (2)
0.3456 cos φ2 + 0.432 cos φ3 = - 0.464
0.3456 sin φ2 + 0.432 sin φ3 = - 0.494
sin φ3= -0,8472; sin φ2= -0,376; cos φ2= -0,9266; cos φ3= 0,5313
Дифференцируя систему (2) по времени получим систему уравнений для определения скорости ω2, ω3:
-L1 ω1sin φ1 - L2 ω2sinφ2 - L3 ω3sin φ3 = 0
L1 ω1cos φ1 +L2 ω2 cos φ2 +L3 ω3 cosφ3 = 0 (3)
ω2 = 2,498 1/с; ω3 = 1,386 1/с
Дифференцируем систему (3) по времени получим систему для определения ускорений ε1, ε2
-L1 ε1sin φ1 - L1 ω1 2cos φ1 - L2 ε2sinφ2 - L2 ω2 2cos φ2 - L3 ε3sin φ3 - L3ω3 2cosφ3= 0
L1 ε1cosφ1 - L1 ω1 2sin φ1 + L2 ε2cosφ2 - L2 ω2 2sin φ2 + L3 ε3cos φ3 - L3ω3 2sinφ3= 0
ε2 =7,45 1/с2; ε2 = 4,76 1/с2
рассмотрим вторую схему
Звенья механизма представляют в виде векторов Li. Механизм замкнут, уравнение замкнутости векторного контура:
L1 + L2 + L3 + L4 = 0 (1)
Проецируя на неподвижной системы координат OX0Y0 получим систему уравнений для определения φ 2, L4:
L1cos φ1 + L2 cos φ2 + L4 = 0
L1sin φ1 +L2 sin φ2 +L3= 0 (2)
sin φ2 = 0,85; сos φ2= 0,53; L4 = 0,12 м
Дифференцируя систему (2) по времени получим систему уравнений для определения скорости ω2, V4:
-L1 ω1sin φ1 - L2 ω2sinφ2 + V4= 0
L1 ω1cos φ1 +L2 ω2 cos φ2 = 0 (3)
ω2 = 3,45 рад/с; V4 = 0.64 м/с
Дифференцируем систему (3) по времени получим систему для определения ускорений ε1, ε2
L1 ε1sin φ1+ L1 ω1 2cos φ1+ L2 ε2sinφ2 + L2 ω2 2cos φ2 + А4= 0
L1 ε1cosφ1 + L1 ω1 2sin φ1 + L2 ε2cosφ2 - L2 ω2 2sin φ2 = 0
ε2 = 4,581 рад/с2 ; А4 = 1,62 м/с2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
