Структурный и кинематический анализ семизвенного рычажного механизма (число подвижных звеньев - 5)

Гвоздева Ксения

Е-433

Лабораторная работа № 1.

Вариант 3-2

Структурный и кинематический анализ рычажного механизма.

Структурный анализ механизма.

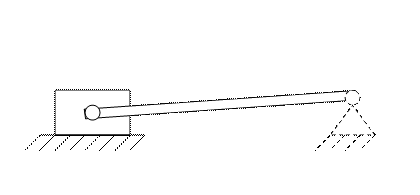
На рис. 1 представлена структурная схема исследуемого семизвенного механизма с пятью подвижными звеньями, где   1 -кривошип,  2-кулиса, 3-коромысло, 4-ползун, 5-шатун,   6 -стойки.

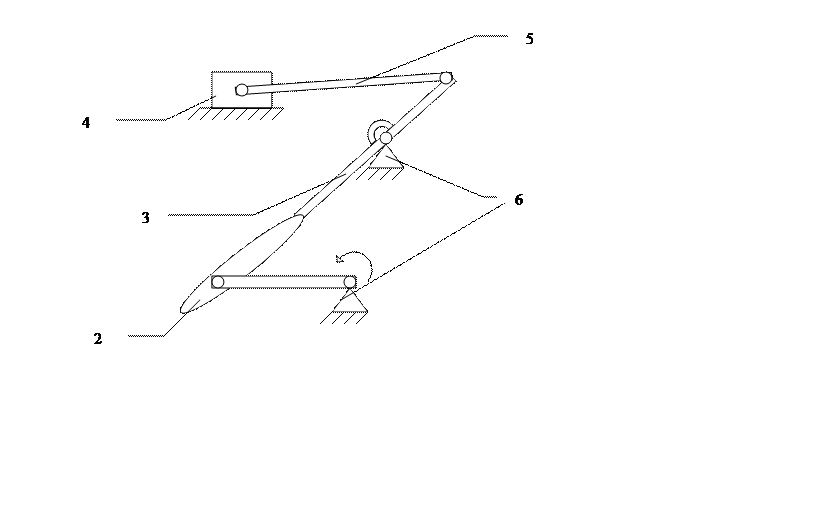
рис.1.

Определение числа степеней свободы механизма по формуле Чебышева для плоских механизмов.

Т.к. в структурной схеме механизма присутствует кинематическая пара 4-го класса, то для  подсчета числа степеней свободы механизма мы добавляем фиктивный ползун (см. рис.2)

W = 3n - 2p₅ - p₄ = 3×5 – 2×7 – 0 = 1,

где n – число подвижных звеньев , p_k- количество кинематических пар k-го класса.

    

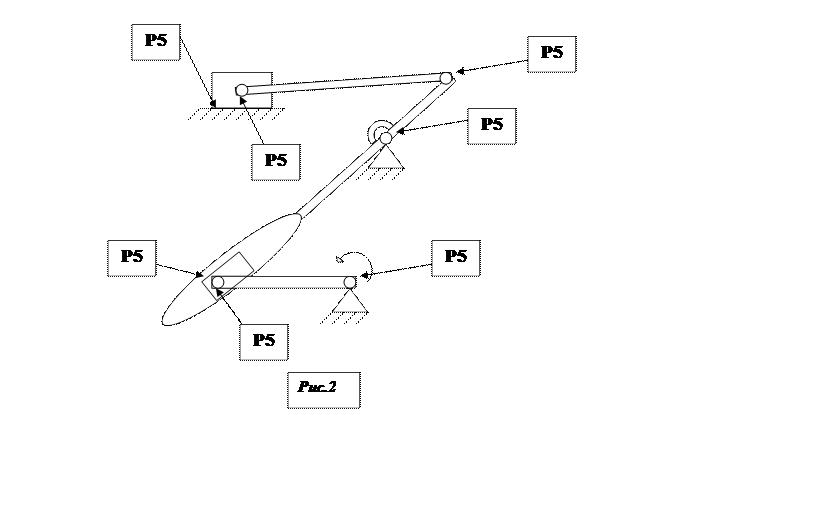
Структурное деление механизма:

Входное звено – кривошип:

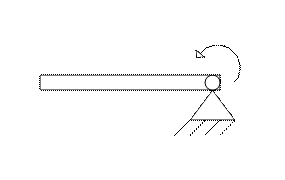     рис.3.

W = 3×1 – 2×1 = 1           

Структурные группы:

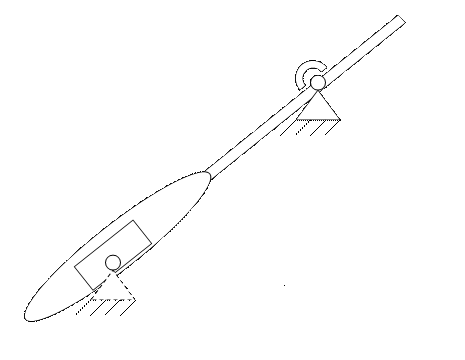                           W = 3×2 – 2×3 = 0

рис.4(а).

W = 3×2 – 2×3 = 0  

рис.4(б).

Кинематический анализ механизма.

Кинематический анализ производиться эксперементально-теоретичеси с использованием разложения в ряд МНК и ряд Фурье. Функцию положения F(φ) выходного штока в зависимости от угла поворота кривошипа 1 получаем экспериментально.

Полагая, что кривошип вращается равномерно с угловой скоростью ω=20 1/с, а, следовательно, φ=ω×t, получаем функцию положения от времени F(t) , её разлагаем в ряды МНК и Фурье, а дифференцированием рядов определяем зависимости для скорости  и ускорения штока.

Таблица экспериментальной зависимости функции перемещения штока  F(φ) с шагом ∆φ=20^° по углу  поворота кривошипа.

φ °	0	20	40	60	80	100	120	140	160	180
Ѕ, мм	69	79,5	89	96	110	113,5	112,5	91,5	69	68
φ °	200	220	240	260	280	300	320	340	360
Ѕ, мм	67,9	91	112,5	112	112	95,7	88	79	69

Шаг по времени при этом: ∆t = ∆φ ∕ω=20×π ∕ (50×180) = 0,007сек.

Обработку данных эксперимента проведем с помощью программного обеспечения для ПЭВМ.

Разложим F(t) в ряд МНК с максимально возможным числом членов:n =n_max=18  и на основании анализа полученного амплитудного спектра (см. рис.5) определим рациональное число членов ряда величину n_r. Варьируя числом  членов ряда скорректируем величину n_r  и получим аппроксимацию дискретной функции перемещения штока (см. рис.6), и ее производные - скорость (см. рис. 7) и ускорение (см. рис. 8)

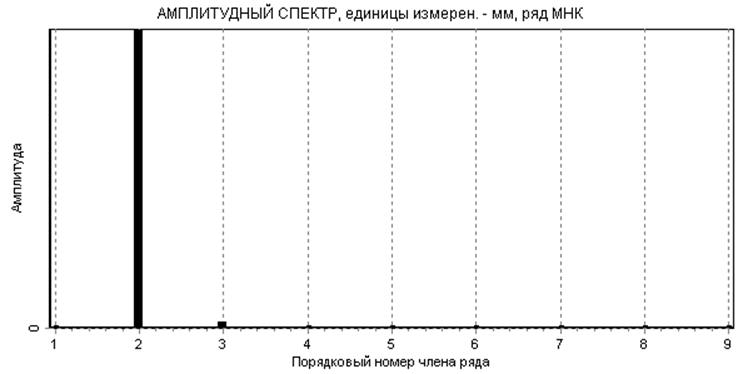
рис.5

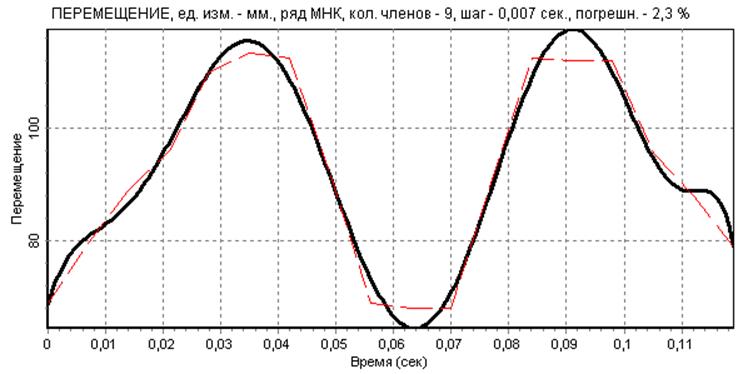
рис.6

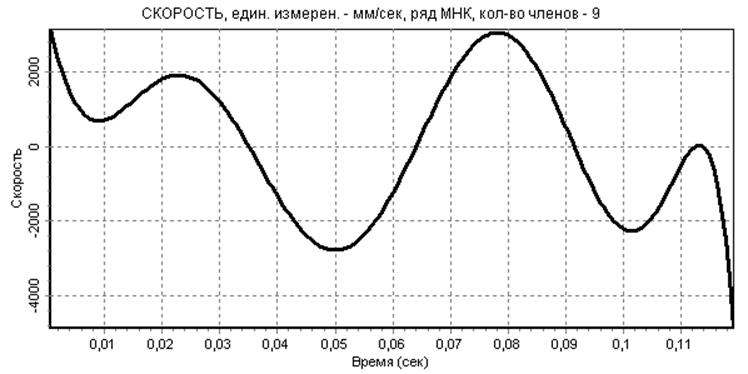
рис.7

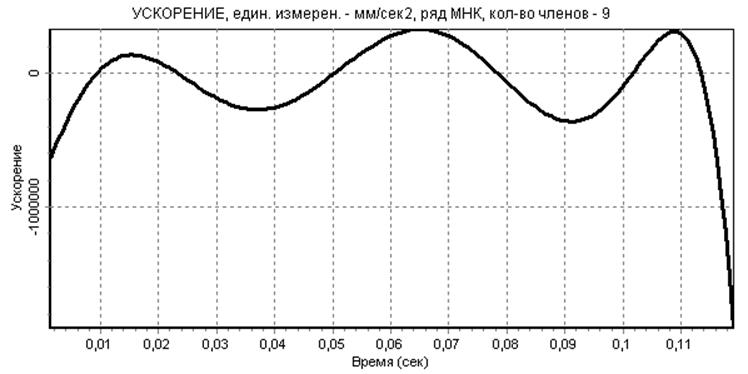
рис.8

Проведенный анализ полученных зависимостей,, показывает, что величина суммарной относительной погрешности  аппроксимации функции является небольшой,. Сама полученная приближенная зависимость «похожа» на исходную, а сами аппроксимированные функции перемещения, скорости и ускорения являются гладкими.

Разложим F(t) в ряд Фурье с максимальновозможным числом гармоник: S=n_max=m/2=18/2=9 (рис.9).В этом случае значения ряда Фурье в узлах практически совпадают с данными эксперимента. Результаты дифференцирования полученной приближенной зависимости представлены на (рис.10) и (рис.11). На графике скорости и особенно ускорения явно видны паразитные осцилляции, вызванные погрешностями замера значений F(t_i).

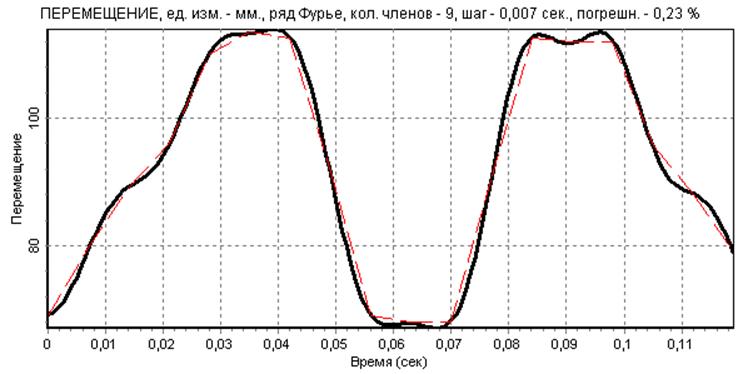
рис.9

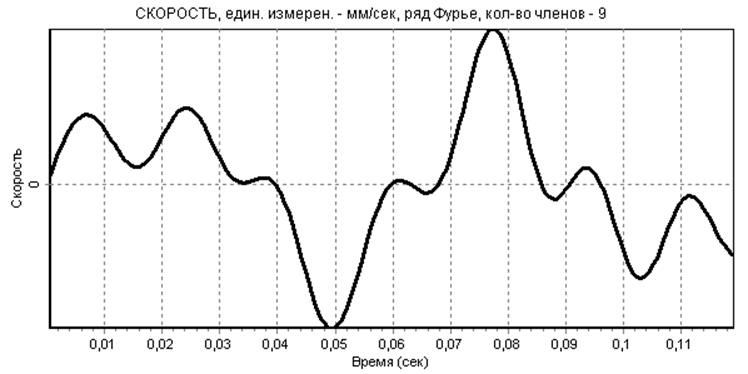
рис.10

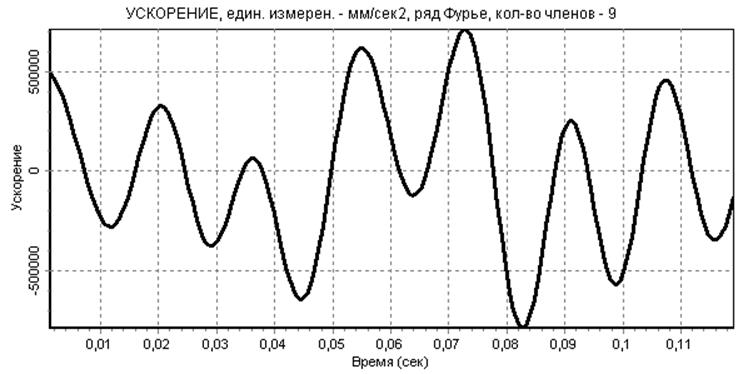
рис.11

Анализ амплитудного спектра полученной функции (см. рис.12) показывает, что наибольший вклад в формирование исследуемой зависимости вносят первые две гармоники, поэтому проведем разложение в ряд и аппроксимацию функции с учетом рационального числа гармоник n_r=2. приближенная функция и результаты ее дифференцирования представлены на рис. 13, 14 и 15.

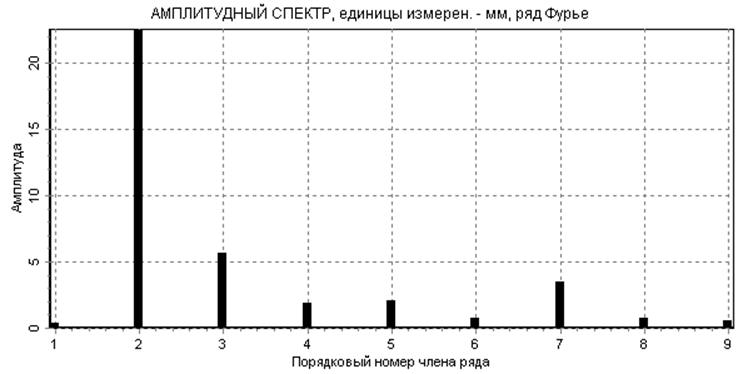
рис.12

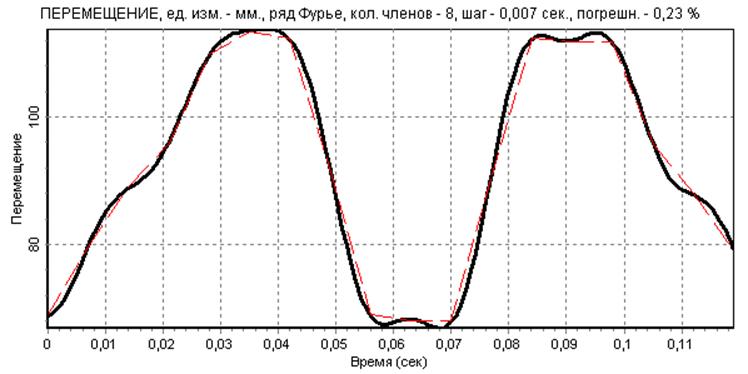
рис.13

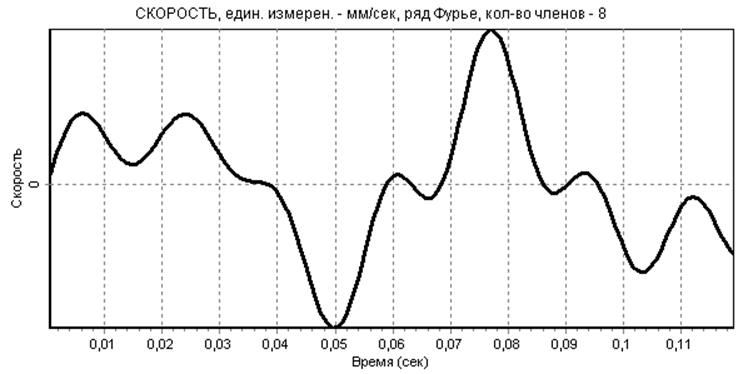
рис.14

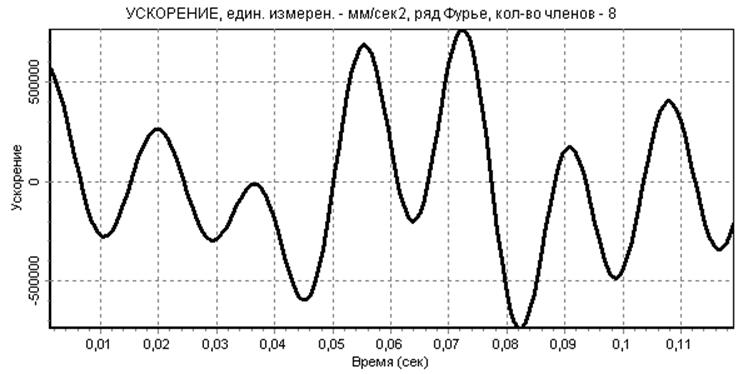
рис.15

Анализ итоговых зависимостей показывает, что величина суммарной относительной погрешности аппроксимации функции является небольшой, а сами аппроксимированные функции перемещения, скорости и ускорения являются гладкими.

Таким образом, ряды МНК и Фурье могут быть успешно применены для решения поставленных задач по аппроксимации заданной дискретной функции, ее сглаживанию и дифференцированию, а также снижению экспериментальных погрешностей.

Лабораторная работа № 2.

Вариант 6-7

Структурный и кинематический анализ кулачкового механизма.

Структурный анализ механизма.