Структурный и кинематический анализ семизвенного рычажного механизма (число подвижных звеньев - 5), страница 2

На рис. 1 представлена структурная схема плоского кулачкового механизма с толкателем, силовым замыканием и роликовым контактом, где 1- кулачок, 2-толкатель, 3- ролик, Р - рабочий профиль, Ц- центровой профиль, R₀-радиус базовой окружности, е- эксцентриситет,γ- угол давления.

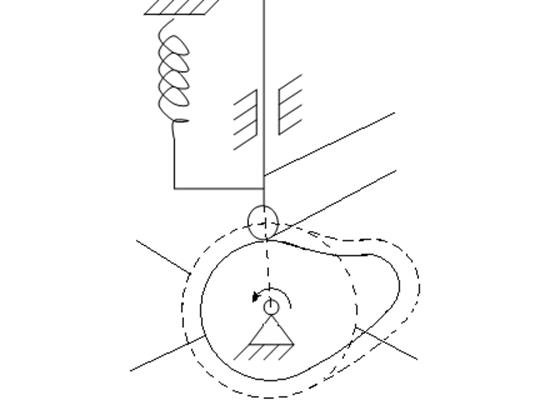
рис.1

Число степеней свободы механизма:

W = 3n - 2p₅ - p₄ = 3×2 – 2×2 – 1 = 1,                                                                                                                                  где n – число подвижных звеньев , p_k- количество кинематических пар k-го класса.

При вычислении числа степеней свободы ролик как пассивное звено и кинематические пары, им образованные, не учитываются.

Механизм имеет четыре фазы работы: удаление, дальний выстой, возврат и ближний выстой. Соответствующие конструктивные углы кулачка β_у,  β_д,  β_в, β_б, обозначены на (рис.1).

На рисунке также показан угол давления γ, измеряемый между вектором реакции R со стороны кулачка на толкатель и вектором скорости толкателя V_T.

Кинематический анализ механизма.

Кинематический анализ производится экспериментально – теоретически с использованием разложения в ряд Фурье. Функцию положения  F(φ) толкателя 2 в зависимости от угла поворота кулачка 1 получаем экспериментально.

Полагая, что кулачок вращается равномерно с угловой скоростью ω=50 1/с, получаем в функцию положения толкателя от времени F(t), разлагаем в ряд Фурье и дифференцированием ряда определяем зависимости для скорости и ускорения толкателя.

В таблице представлена  экспериментальная зависимость функции перемещения толкателя  F(φ) с шагом ∆φ=10^°  по углу поворота кулачка.

φ  °	0	10	20	30	40	50	60	70	80	90
Ѕ, м	0,0095	0,0095	0,0095	0,0095	0,0095	0,011	0,0115	0,0285	0,0405	0,05
φ  °	100	110	120	130	140	150	160	170	180	190
Ѕ, м	0,055	0,0555	0,0565	0,045	0,038	0,031	0,025	0,0205	0,016	0,0125
φ  °	200	210	220	230	240	250	260	270	280	290
Ѕ, м	0,01	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095
φ  °	300	310	320	330	340	350	360
Ѕ, м	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095	0,0095

Шаг по времени при этом: ∆t = ∆φ ∕ω=10×π ∕ (50×180) = 0,0035сек.

Обработку данных эксперимента проведем с помощью программного обеспечения для ПЭВМ.

На первом этапе разложим дискретную функцию F(t) в ряд с максимально возможным числом членов: s=n_max=m/2=36/2=18. В этом случае значения ряда Фурье в узлах практически совпадают с данными эксперимента. Полученные результаты расчетов представлены на рис. 2,3,4,5.

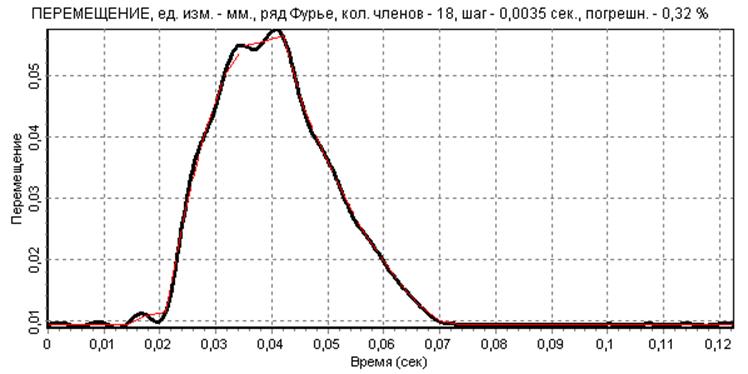
рис.2

Видно, что полученный график перемещения является однозначно негладким. На графике скорости и особенно ускорения явно видны паразитные осцилляции, вызванные погрешностями замера значений экспериментальной функции F(t_i), что приводит к необходимости сглаживания этих зависимостей. Кроме того, на графике перемещения, скорости и ускорения неудовлетворительно аппроксимированы участки фаз выстоя.

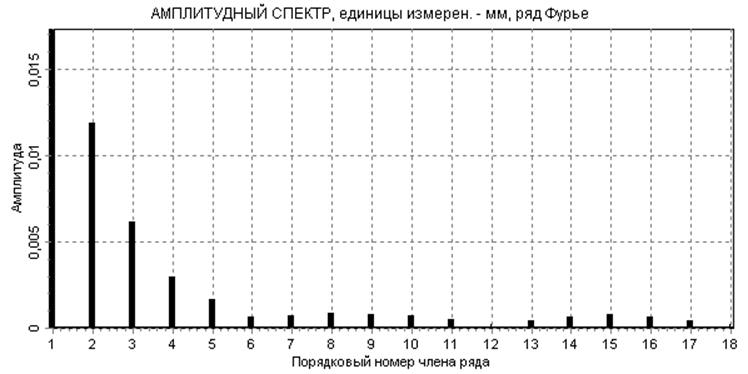
рис.3

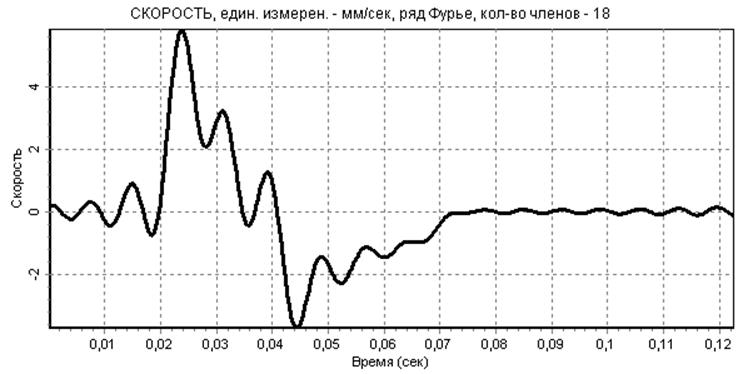
рис.4

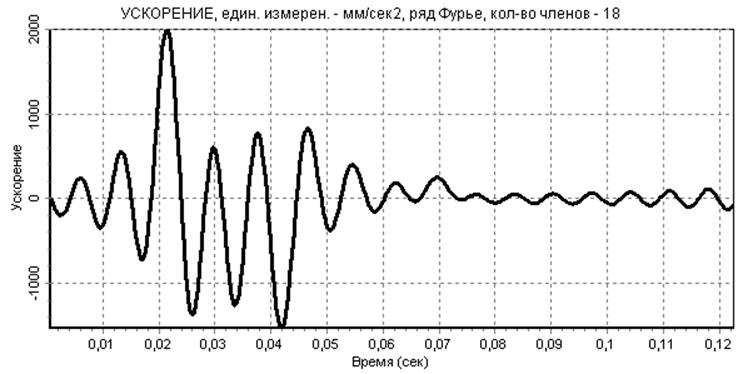
рис.5

Анализ амплитудного спектра функции (см. рис.3) показывает, что наибольший вклад в формирование приближенной зависимости, полученной с помощью ряда Фурье, вносят  первые 5 гармоник, однако варьирование числом членов ряда показало, что наилучшие результаты (с точки зрения минимизации погрешности и «похожести» графика перемещения) достигаются при 17 членах ряда. На рис. 6,7,8 показаны результаты такой аппроксимации исходной дискретной функции перемещения и ее двукратного дифференцирования.

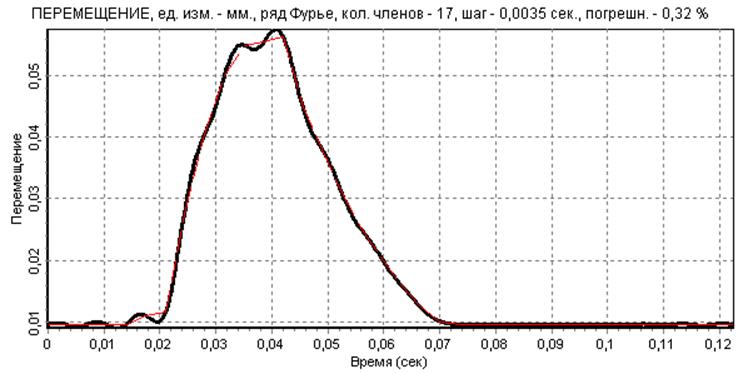
рис.6

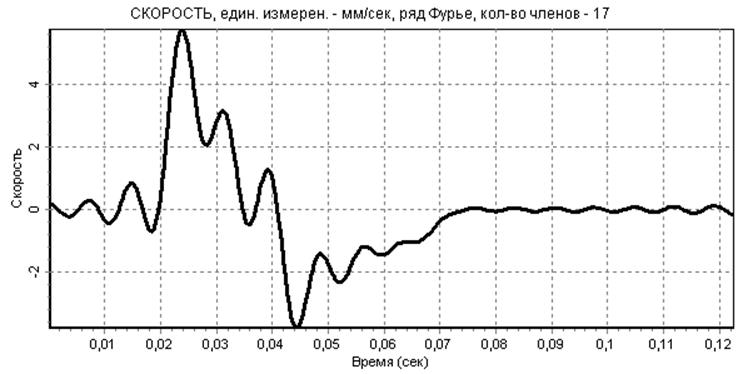
рис.7

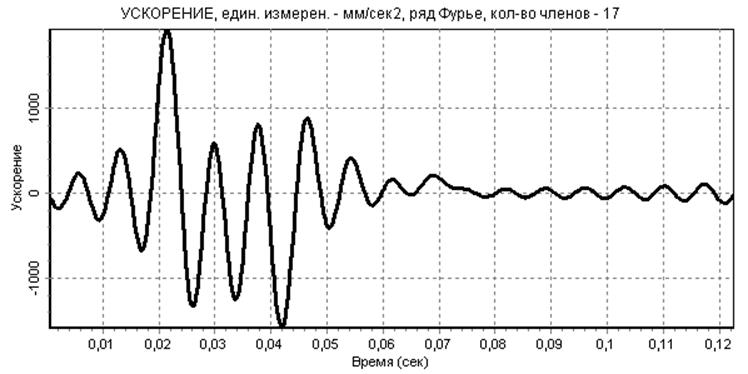
рис.8

Анализ представленных зависимостей показывает, что удалось несколько сгладить погрешности эксперимента. Функция удовлетворительно аппроксимирована лишь на фазах удаления и возврата, однако приемлемо аппроксимировать функцию и ее производные на фазах выстоя не удалось, на этих участках все равно наблюдаются осцилляции.