Кинематический анализ механизма. Определение зависимости скорости и ускорения кулисы

2. Кинематический анализ механизма

⁰	0	10	20	30	40	50	60	70	80	90	100	110	120
F()	25	27	27	25,8	10	8	7	7	7	7	7	7	7
⁰	130	140	150	160	170	180	190	200	210	220	230	240	250
F()	7	7	7	7	7	7	7	7	7	7,6	8	9	10
⁰	260	270	280	290	300	310	320	330	340	350	360
F()	10,5	11,5	12,5	13,5	14,5	16,5	18	19,5	21	23	25

Кинематический анализ производится экспериментально-теоретически. Функцию положения F() коромысла 2 в зависимости от угла поворота кулачка 1 получаем экспериментально. Её таблица значений  представлена в табл. 1.

Полагая, что кулачок вращается равномерно с угловой скоростью , а, следовательно , получаем функцию положения от времени F(t), её раскладываем в ряд Фурье и дифференцированием ряда определяем зависимость скорости V(t) и ускорения a(t) кулисы. При этом необходимо решить вопрос о достаточном числе членов ряда.

Разложение функции в ряд Фурье означает её приближённую замену тригонометрическим полиномом вида:

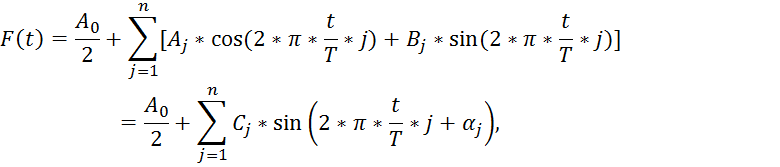
где  с – время полного оборота кулачка,

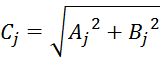 – амплитуда сигнала на j-ой частоте.

Частота сигнала для j-ой гармоники:  .

Поскольку в данном случае функция F(t) задана таблицей значений в конечном числе точек m, то максимальное число членов ряда:

.

Формулы для вычисления коэффициентов ряда Фурье при табличном задании функции:

 и

,

Где  – значения функции, где i=0,1,2,…, m-1.

Рассчитаем шаг по времени, переведя сначала угол из градусов в радианы:

.

Подставим полученное значение в формулу:

 с.

Дальнейшая обработка будет проводиться с помощью программы ApproxFSP.

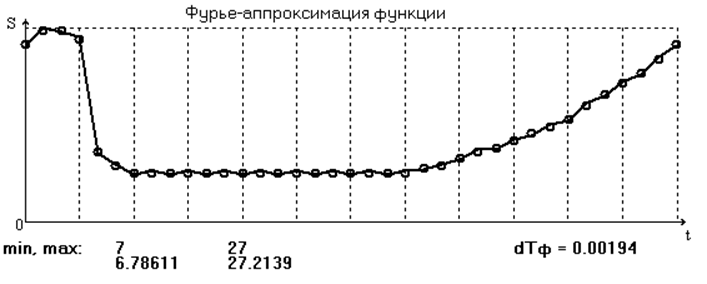
Разложим заданную таблицей функцию в ряд Фурье с 18 учитываемыми членами (рис. 4).

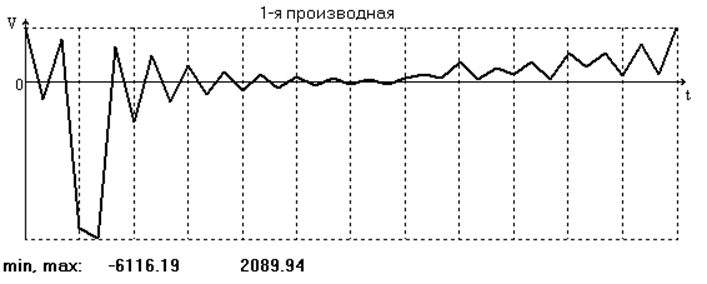
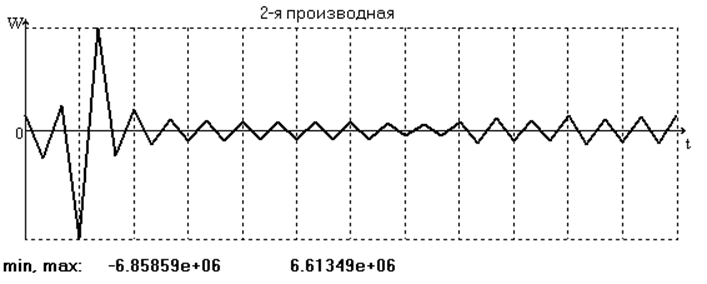
Кружочками на графике  обозначены дискретные экспериментальные значения функции. Результаты дифференцирования ряда по времени представлены на графиках скорости (рис. 5) и ускорения (рис. 6) и в табл. 2.

 

i    t, c     S, мм       Ряд      Произв-я 1  Произв-я 2

0  0.000e+00  2.500e+01  2.446e+01  1.416e+03  4.591e+05

1  1.940e-03  2.700e+01  2.758e+01  1.431e+03 -6.436e+05

2  3.880e-03  2.700e+01  2.822e+01 -1.175e+03 -1.851e+06

3  5.820e-03  2.580e+01  2.256e+01 -4.418e+03 -1.108e+06

4  7.760e-03  1.000e+01  1.318e+01 -4.568e+03  9.513e+05

5  9.700e-03  8.000e+00  6.918e+00 -1.645e+03  1.678e+06

6  1.164e-02  7.000e+00  6.318e+00  6.236e+02  4.783e+05

7  1.358e-02  7.000e+00  7.595e+00  3.580e+02 -5.362e+05

8  1.552e-02  7.000e+00  7.340e+00 -4.908e+02 -1.607e+05

9  1.746e-02  7.000e+00  6.526e+00 -1.676e+02  3.800e+05

10  1.940e-02  7.000e+00  6.836e+00  3.816e+02  6.978e+04

11  2.134e-02  7.000e+00  7.395e+00  7.024e+01 -2.986e+05

12  2.328e-02  7.000e+00  7.063e+00 -3.157e+02 -1.604e+04

13  2.522e-02  7.000e+00  6.662e+00 -9.083e+00  2.489e+05

14  2.716e-02  7.000e+00  7.004e+00  2.705e+02 -2.174e+04

15  2.910e-02  7.000e+00  7.295e+00 -3.529e+01 -2.144e+05

16  3.104e-02  7.000e+00  6.945e+00 -2.360e+02  5.181e+04

17  3.298e-02  7.000e+00  6.741e+00  7.183e+01  1.880e+05

18  3.492e-02  7.000e+00  7.099e+00  2.067e+02 -7.985e+04

19  3.686e-02  7.000e+00  7.222e+00 -1.094e+02 -1.670e+05

20  3.880e-02  7.000e+00  6.853e+00 -1.730e+02  1.252e+05

21  4.074e-02  7.000e+00  6.882e+00  2.349e+02  2.189e+05

22  4.268e-02  7.600e+00  7.613e+00  4.346e+02 -2.973e+04

23  4.462e-02  8.000e+00  8.306e+00  2.641e+02 -7.755e+04

24  4.656e-02  9.000e+00  8.802e+00  3.191e+02  1.346e+05