Кинематический анализ механизма. Определение зависимости скорости и ускорения кулисы, страница 2

25  4.850e-02  1.000e+01  9.711e+00  6.031e+02  8.993e+04

26  5.044e-02  1.050e+01  1.088e+01  5.240e+02 -1.549e+05

27  5.238e-02  1.150e+01  1.160e+01  2.419e+02 -6.064e+04

28  5.432e-02  1.250e+01  1.215e+01  4.231e+02  2.215e+05

29  5.626e-02  1.350e+01  1.340e+01  8.294e+02  1.196e+05

30  5.820e-02  1.450e+01  1.504e+01  7.737e+02 -1.409e+05

31  6.014e-02  1.650e+01  1.630e+01  5.778e+02  1.246e+04

32  6.208e-02  1.800e+01  1.763e+01  8.731e+02  2.326e+05

33  6.402e-02  1.950e+01  1.966e+01  1.121e+03 -5.081e+04

34  6.596e-02  2.100e+01  2.151e+01  7.134e+02 -2.692e+05

35  6.790e-02  2.300e+01  2.261e+01  5.811e+02  2.212e+05

36  6.984e-02  2.500e+01  2.446e+01  1.416e+03  4.591e+05

На полученных графиках явно видны паразитные осцилляции, вызванные погрешностями замера значений . Возникает необходимость сглаживания этих зависимостей. Кроме того, на графике скорости и особенно ускорения неудовлетворительно аппроксимированы участки фаз выстоя.

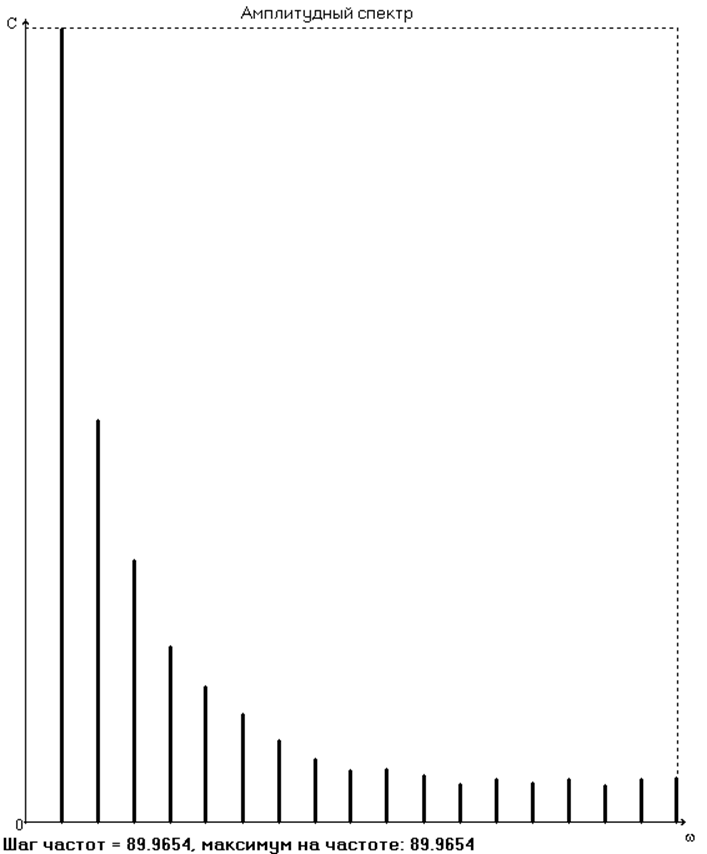
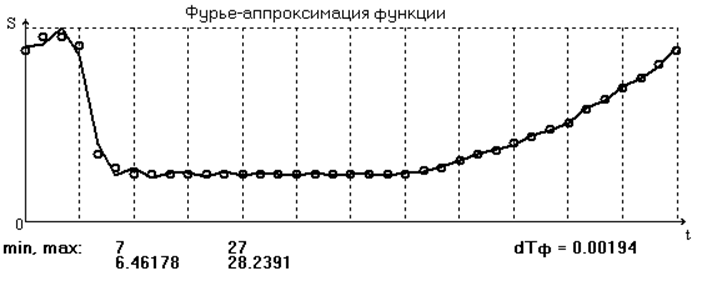
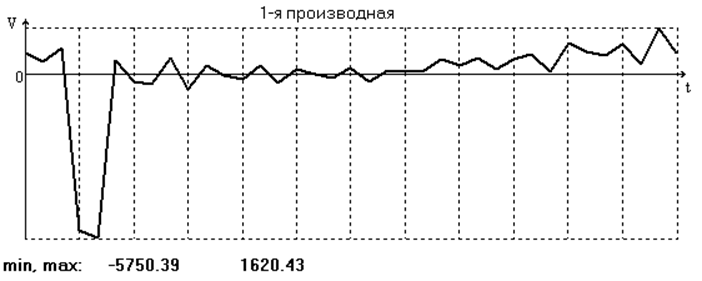
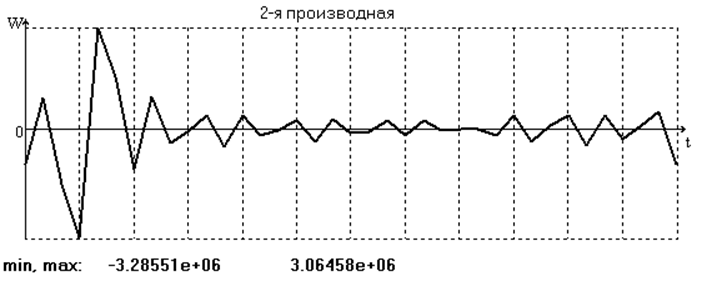
Анализ амплитудного спектра исследуемой функции не даёт чёткого представления о том, какие осцилляции являются в достаточной степени паразитными, однако исследования показали, что наилучшее результаты достигаются при 14 членах ряда. На рис. 8, 9, 10 и в табл. 4 представлены результаты двукратного дифференцирования ряда  в этом случае.

 

i     t, c       S, м       Ряд    Произв-я 1  Произв-я 2

0  0.000e+00  2.500e+01  2.560e+01  7.458e+02 -1.062e+06

1  1.940e-03  2.700e+01  2.604e+01  4.389e+02  9.513e+05

2  3.880e-03  2.700e+01  2.824e+01  9.401e+02 -1.656e+06

3  5.820e-03  2.580e+01  2.441e+01 -5.487e+03 -3.286e+06

4  7.760e-03  1.000e+01  1.138e+01 -5.750e+03  3.065e+06

5  9.700e-03  8.000e+00  6.793e+00  4.870e+02  1.614e+06

6  1.164e-02  7.000e+00  7.906e+00 -3.016e+02 -1.210e+06

7  1.358e-02  7.000e+00  6.462e+00 -3.891e+02  9.996e+05

8  1.552e-02  7.000e+00  7.177e+00  6.050e+02 -4.242e+05

9  1.746e-02  7.000e+00  7.113e+00 -5.440e+02 -9.943e+04

10  1.940e-02  7.000e+00  6.715e+00  3.222e+02  4.374e+05

11  2.134e-02  7.000e+00  7.325e+00 -4.692e+01 -5.441e+05

12  2.328e-02  7.000e+00  6.749e+00 -1.886e+02  4.418e+05

13  2.522e-02  7.000e+00  7.106e+00  3.198e+02 -2.037e+05

14  2.716e-02  7.000e+00  7.055e+00 -3.217e+02 -7.135e+04

15  2.910e-02  7.000e+00  6.822e+00  2.106e+02  2.875e+05

16  3.104e-02  7.000e+00  7.226e+00 -3.495e+01 -3.778e+05

17  3.298e-02  7.000e+00  6.810e+00 -1.403e+02  3.206e+05

18  3.492e-02  7.000e+00  7.084e+00  2.535e+02 -1.434e+05

19  3.686e-02  7.000e+00  7.054e+00 -2.622e+02 -8.654e+04

20  3.880e-02  7.000e+00  6.820e+00  1.489e+02  2.733e+05

21  4.074e-02  7.000e+00  7.251e+00  1.214e+02 -2.017e+05

22  4.268e-02  7.600e+00  7.356e+00  1.646e+02  2.854e+05

23  4.462e-02  8.000e+00  8.161e+00  5.417e+02 -5.031e+04

24  4.656e-02  9.000e+00  8.976e+00  3.319e+02  3.204e+04

25  4.850e-02  1.000e+01  9.876e+00  5.965e+02  2.579e+04

26  5.044e-02  1.050e+01  1.074e+01  2.008e+02 -2.132e+05

27  5.238e-02  1.150e+01  1.122e+01  5.349e+02  4.492e+05

28  5.432e-02  1.250e+01  1.274e+01  7.341e+02 -3.840e+05

29  5.626e-02  1.350e+01  1.338e+01  1.092e+02  1.383e+05

30  5.820e-02  1.450e+01  1.447e+01  1.122e+03  4.451e+05

31  6.014e-02  1.650e+01  1.668e+01  8.076e+02 -5.258e+05

32  6.208e-02  1.800e+01  1.775e+01  6.553e+02  4.355e+05

33  6.402e-02  1.950e+01  1.970e+01  1.081e+03 -3.163e+05

34  6.596e-02  2.100e+01  2.097e+01  3.727e+02  1.262e+05

35  6.790e-02  2.300e+01  2.275e+01  1.620e+03  5.269e+05

36  6.984e-02  2.500e+01  2.560e+01  7.458e+02 -1.062e+06

Выводы по работе

1.  Ряд Фурье хорошо аппроксимирует лишь достаточно гладкие функции.

2.  В данном случае функция аппроксимирована удовлетворительно во всём диапазоне.

3.  Производные аппроксимированы с ощутимыми погрешностями, которые в большей степени заметны на фазах удаления и возврата. Особенно это касается ускорения.

4.  Если функция состоит из нескольких участков, то целесообразно аппроксимировать каждый участок в отдельности.