Физический смысл коэффициента перекрытия: число пар зубьев одновременно находящихся в зацеплении. С другой стороны, коэффициент перекрытия – величина дробная. Например, коэффициент перекрытия равный 1,25 показывает, что в зацеплении всегда находится одна пара зубьев и какое-то время (а именно 25% от времени работы зубчатого механизма) находятся в зацеплении две пары зубьев. Коэффициент перекрытия влияет на нагрузку зуба по рабочему участку эвольвентного профиля.
Нужно отметить, что в зацеплении могут находиться
колеса только одного модуля. Например, модуль одного колеса 
мм, значит модуль второго колеса,
находящегося в зацеплении, тоже должен быть равен
5 мм.
Вопросы для самопроверки к теме 3:
1. Основные параметры и свойства эвольвенты.
2. Параметры прямозубого зубчатого колеса.
3. Что такое делительная и основная окружности?
4. Что такое модуль колеса?
5. Положительные, нулевые, отрицательные колеса – что между ними общего, чем они отличаются?
6. Параметры эвольвентного зубчатого зацепления.
7. Свойства эвольвентного зацепления.
8. Методы изготовления зубчатых колес.
9. Параметры зубчатой рейки.
10. Явление подрезания зубьев, корригирование колес, задачи корригирования колес.
11. Расположение окружностей при зацеплении нулевых и корригированных колес.
12. Коэффициент перекрытия. В чем заключается его физический смысл?
Тема 4. Сложные зубчатые механизмы (3), гл.10, §57, 58, 60, 61; (2), гл.13, §58 (4); (1), гл.15, §15.1.
Сложные зубчатые механизмы. Назначение. Простейшие зубчатые механизмы или одноступенчатые передачи. Понятие о передаточном отношении. Сложные ступенчатые зубчатые механизмы. Определение передаточного отношения.
Планетарные механизмы. Определение, назначение, степень подвижности. Определение передаточного отношения (аналитический - метод Виллиса и графический метод). Построение плана чисел оборотов планетарного механизма.
Типовые схемы планетарных механизмов. Силовой расчет зубчатых механизмов – простых одноступенчатых и планетарных. Расчет планетарных передач, условия сборки, соседства, соосности.
Определение КПД зубчатых передач: простых одноступенчатых и планетарных. Области применения планетарных редукторов, в том числе в конструкции самолета.
Дифференциальные механизмы. Определение, назначение, степень подвижности. Определение передаточного отношения дифференциальных механизмов: аналитический и графический методы.
Данная тема является очень важной и необходимой при подготовке материалов к выполнению курсового проекта по дисциплине «Детали машин» студентами 4 курса специальности 160901.
1. Проработку материала по этой теме необходимо начать с определения «что такое редуктор?»
Редуктор – это зубчатый механизм, который
устанавливают между двигателем и исполнительным механизмом (например, ………..) и который предназначен для уменьшения частоты
вращения (числа оборотов) и увеличения крутящего момента на выходном (ведомом
валу). На входной (ведущий) вал мощность 
подается
от двигателя. Значит, редуктор согласует параметры (угловая скорость и крутящий
момент) двигателя и исполнительного механизма, соблюдая условие
Это равенство является энергетическим равенством редуктора.
2. Кинематической характеристикой редуктора является передаточное отношение «U».
Передаточное отношение от ведущего колеса к ведомому – это отношение угловой скорости (числа оборотов) вала ведущего колеса к угловой скорости (числу оборотов) вала ведомого колеса.
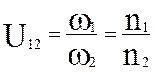
Или отношение числа зубьев (радиусов) ведомого колеса
к числу зубьев (радиусов) ведущего 
колеса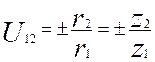 
В этом случае передаточное отношение имеет знак плюс « + », если зацепление двух колес – внутреннее, и знак минус « - », если зацепление двух колес внешнее.
Физический смысл знака передаточного отношения:
Знак плюс « + » - направления вращения входного и выходного вала одинаковы; знак минус « - » - вращения входного и выходного вала направлены в разные стороны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.