Теория механизмов и машин: Методическое пособие для выполнения контрольной работы и подготовки к сдаче дифференцированного зачета, страница 2

·  Полное ускорение любой точки звена состоит из нормального и тангенциального ускорений

                   

.

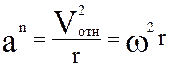Нормальное ускорение параллельно радиусу и направлено к центру вращения

,

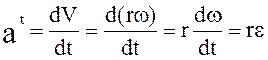e - угловое ускорение звена – это тоже кинематическая характеристика вращательного движения.

Если w = Const, e = 0.

Плоско-параллельное движение твердого тела:

·  Скорость любой точки звена, совершающего плоско-параллельное движение, геометрически слагается из скорости полюса (m.А) и скорости вращения вокруг полюса. За полюс всегда выбирается точка звена (т. А), скорость которой известна.

.

·  Ускорение любой точки может быть представлено как и скорость: ускорение точки геометрически слагается из ускорения полюса и ускорения вращения вокруг полюса.

.

Вопросы для самопроверки к теме 1:

1.  Что такое механизм, деталь, кинематическая пара, кинематическая цепь?

2.  Формула Чебышева – структурная формула плоской кинематической цепи.

3.  Какой принцип положен в основу образования плоских механизмов по Ассуру?

4.  Как определяется класс механизмов по Ассуру?

5.  Какая существует аналитическая зависимость между угловой и линейной скоростями, угловым и линейным ускорениями при вращательном движении твердого тела?

6.  Определение скоростей и ускорений точек звеньев механизма методом планов.

7.  Составление векторных уравнений для определения скоростей и ускорений точек, принадлежащих одному звену или разным звеньям механизма.

8.  Как используется план скоростей и ускорений для определения величины и направления угловых скоростей и ускорений звеньев механизма?

9.  Теорема подобия для скоростей и ускорений точек одного звена.

10.  Свойства планов скоростей и ускорений.

Тема 2. Силовой расчет рычажных механизмов (1), гл.5, §5.1, 5.2; (3), гл.11, §66, 67.

Кинетостатический метод силового расчета плоских механизмов. Задачи силового расчета. Силовые воздействия на механизм (внешние и внутренние силы), инерционные нагрузки на звенья, применение принципа Д’Аламбера.

Вопросы для самопроверки к теме 2:

1.  Задачи силового расчета рычажных механизмов.

2.  Силовые воздействия на механизм, внешние и внутренние силы.

3.  Определение сил инерции, действующих на звенья механизма.

4.  Определение пар сил инерции, действующих на звенья механизма.

Тема 3. Цилиндрические зубчатые передачи (3), гл.8, §44-47, §48-52.

Цилиндрические зубчатые передачи. Общие сведения о зубчатых механизмах. Назначение, виды зубчатых механизмов. Эвольвента окружности, ее свойства и уравнение.

Параметры прямозубого зубчатого колеса.

Прямозубое внешнее эвольвентное зацепление. Параметры и свойства. Качественные показатели передачи. Коэффициент перекрытия. Методы изготовления зубчатых колес, их достоинства и недостатки.

Изготовление зубчатых колес инструментальной рейкой. Минимальное число зубьев на колесе при отсутствии подрезания. Корригирование зубчатых колес, цель и виды корригирования. Типы передач.

При изучении данной темы необходимо учесть:

1. Основным параметром эвольвентного зубчатого колеса является модуль  m (мм). Все остальные параметры колеса прямым или косвенным образом зависят от модуля. Например, диаметр делительной окружности колеса d = mZ, радиус основной окружности 

Необходимо помнить – межосевое расстояние при зацеплении двух «нулевых» колес складывается из суммы начальных окружностей

Если колеса «нулевые», то радиусы начальных окружностей колес равны радиусам делительных окружностей, то есть ,  , значит межосевое расстояние:

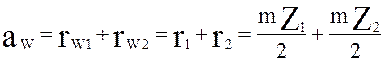
2. Для зубчатого зацепления очень важную роль играет коэффициент перекрытия – это один из качественных показателей работы любой зубчатой передачи.