напряженность поля, создаваемого каждым зарядом в отдельности.
§1.4 Линии напряженности электрического поля.
Для графического изображения электростатических полей применяют метод силовых линий.
Силовыми линиями(линиями напряженности) называются линии, касательные к которым в каждой точке совпадают с напавлением вектора напряженности поля в этой точке.
Силовые линии считаются направленными так же, как вектор напряженности. Они нигде не пересекаются, так как в каждой точке поля вектор Е имеет лишь одно направление.
Силовые линии не тождественны траекториям движения легких заряженных частиц в электрицеском поле. В каждой точке траектории частицы по касательной к траектории направлена скорость. По касательной к силовой синии направлена сила, действующая на заряженную частицу, а следовательно, и ускорение частицы.
§1.5 Поток напряженности.
Элементарным потоком напряженности электрического поля сквозь малый участок площадью dS поверхности, проведенной в поле, называется физическая величина
![]() ,где
,где
![]() -
вектор напряженности электрического поля в точках площадки dS,
-
вектор напряженности электрического поля в точках площадки dS,
n – единичный вектор, нормальный к площадке dS,
![]() -
проекция вектора Е на направление вектора n.
-
проекция вектора Е на направление вектора n.
Например, для
электростатического поля точечного заряда в вакууме 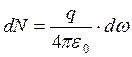 , где
, где
![]() -
телесный угол, под которым площадка dS видна из точки нахождения заряда
q.
-
телесный угол, под которым площадка dS видна из точки нахождения заряда
q.
Поток напряженности электрического поля N сквозь поверхность S равен алгебраической сумме потоков сквозь все малые участки этой поверхности:
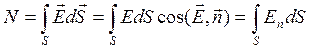 .
.
При этом все векторы n нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S. Например, в случае замкнутой поверхности S вес векторы n нормалей должны быть либо внешними, либо внутренними.
§1.6 Теорема Остроградского-Гаусса.
Поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность, проведенную в поле, пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью.
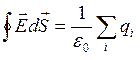 , где
, где ![]() - электрическая постоянная, а все векторы dS
направлены вдоль внешних нормалей к замкнутой поверхности интегрирования
S, которую называют гауссовой поверхностью.
- электрическая постоянная, а все векторы dS
направлены вдоль внешних нормалей к замкнутой поверхности интегрирования
S, которую называют гауссовой поверхностью.
Частные случаи:
1. Напряженность поля бесконечной равномерно заряженной плоскости:
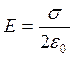 , где
, где ![]() - электрическая постоянная,
- электрическая постоянная,
![]() -
поверхностная плотность заряда.
-
поверхностная плотность заряда.
2.
Напряженность поля двух
параллельных заряженных плоскостей: 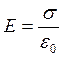 .
.
3.
Напряженность поля бесконечной
равномерно заряженной нити: 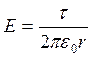 , где
, где ![]() - электрическая постоянная,
- электрическая постоянная,
![]() -
линейная плотность заряда,
-
линейная плотность заряда,
r – расстояние от нити до точки, в которой измеряется напряженность.
4. Напряженность поля полого
равномерно заряженного по поверхности цилиндра: ![]() , если r<R,
, если r<R, 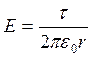 , если r
, если r![]() R, где r – расстояние от
оси цилиндра до точки, в которой находится напряженность поля,
R, где r – расстояние от
оси цилиндра до точки, в которой находится напряженность поля,
R – радиус цилиндра,
![]() -
линейная плотность заряда,
-
линейная плотность заряда,
![]() -
электрическая постоянная.
-
электрическая постоянная.
5.
Напряженность поля заряженной
сферы: ![]() , если r<R,
, если r<R,
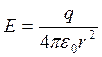 , если r
, если r![]() R.
R.
6.
Напряженность поля шара, равномерно
заряженного по объему: 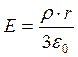 , где
, где ![]() - объемная плотность заряда,
- объемная плотность заряда,
r – расстояние от центра сферы до точки, в которой ищется напряженность,
![]() - электрическая постоянная.
- электрическая постоянная.
§1.7 Работа электрических сил. Потенциал. Разность потенциалов.
Работа dA,
совершаемая кулоновскими силами при малом перемещении dl точечного
заряда q в электростатическом поле, равна ![]() , где
, где
E – напряженность поля в месте нахождения заряда q,
Работа кулоновских сил при
конечном перемещении заряда q из точки 1 в точку 2 равна 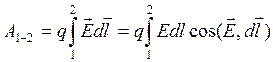 .
.
Для поля одного точечного
заряда q в вакууме работа по его перемещению из то чки 1 в
точку 2 равна 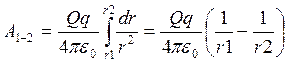 , где
, где
r1 и r2 – расстояния от точек 1 и 2 до заряда q.
Для одноименных зарядов Q и q работа кулоновских сил отталкивания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.