Анализ погрешностей бескарданных инерциальных измерительных модулей, страница 4

                                                                              (9.3.12)

Из (9.3.12) видно, что ось  описывает в картинной плоскости  окружность радиусом  с центром в точке, определяемой координатами  (рис.3.2).

Для дисперсий (учитываются только основные составляющие):

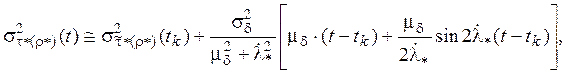
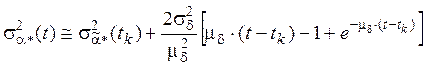.                                                        (9.3.11)

Погрешности аналога вертикали

Проведем анализ погрешностей северного канала аналога вертикали БИИМ на ДУС с учетом их демпфирования по данным относительного лага и принятых ранее допущений. В этом случае его приближенную модель погрешностей представим в виде

   

где

,      ,

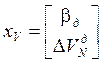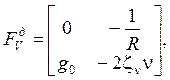
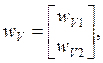
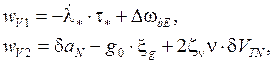                                                                  (9.3.12)

Собственные значения матрицы  (собственные частоты системы) найдем из характеристического уравнения

 или                                                                 (9.3.13)

где  

Откуда

                                                                                            (9.3.14)

Легко видеть, что при  система (9.3.12) обладает асимптотической устойчивостью. При этом при  переходный процесс в системе будет апериодическим, а при  - колебательным:  с периодом

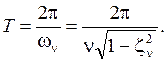                                                                                                 (9.3.15)

Переходная матрица стационарной системы (9.3.12) может быть найдена как обратное преобразование  Лапласа обратной матрицы  (здесь s – оператор Лапласа), т.е.

 

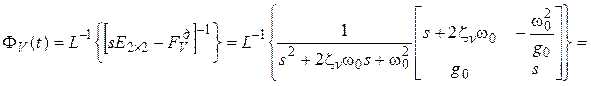
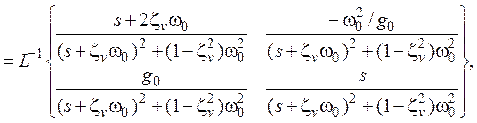
(здесь 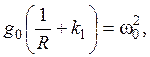  из уравнения )

Можно показать, что переходная матрица состояния системы при ,   и при принятых допущениях будет равна

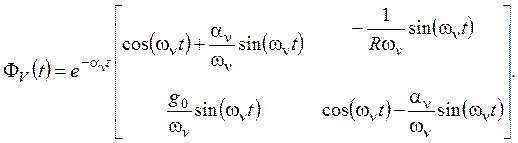                                      (9.3.16)

Тогда в соответствии с решением вида (9.1.5) переходный процесс в системе из-за ненулевых начальных условий при  описывается следующим образом:

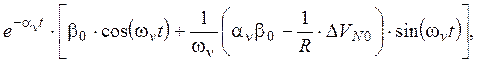
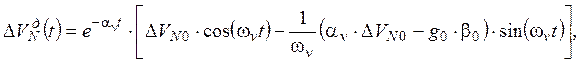                           (9.3.17)

при этом время переходного процесса приближенно будет равно

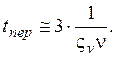                                                                                                            (9.3.18)

Полагая, что входные возмущения  в проекциях на оси географической системы координат  содержат составляющие:

·  детерминированные в одном пуске БИИМ:

 - для дрейфов гироскопов и погрешностей акселерометров (систематические и колебательные с частотами качки и модуляционного вращения ИБ БИИМ для случая, когда )

, ();

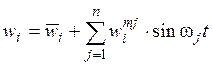 - для погрешностей аналога ИСК (систематические и колебательные):

·  флуктуационные, аппроксимированные марковскими процессами первого порядка с параметрами  соответственно для дрейфов гироскопов и погрешностей акселерометров () и белым шумом интенсивности  для погрешностей лага;

·  а УОЛ и погрешности относительного лага представим в виде суммы систематических составляющих соответственно  (глобальные и региональные составляющие УОЛ) и  (инструментальные погрешности лага) и флуктуационных  (локальные изменения УОЛ) и  (флуктуации морских течений), аппроксимируемых марковскими процессами первого порядка с параметрами соответственно  и ;

для погрешностей аналога вертикали в установившемся режиме согласно решениям (9.1.5) и (9.1.9), получим следующие аналитические зависимости.

Для средних значений:

    

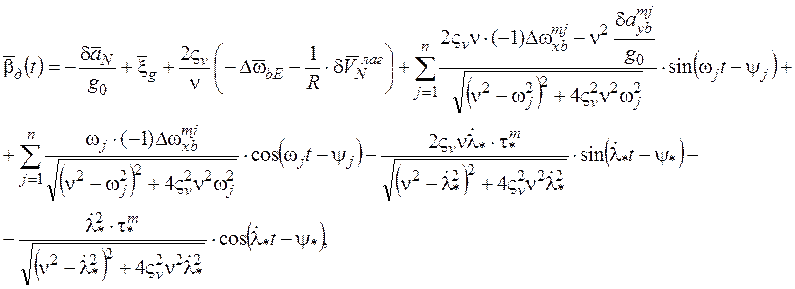
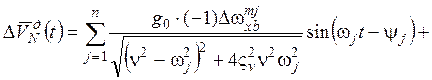
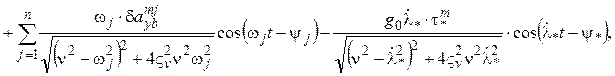                  (9.3.19)

где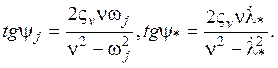  

Для дисперсий:

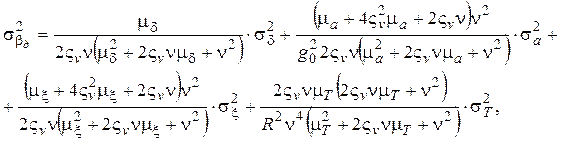
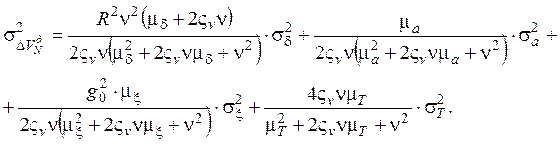                               (9.3.20)

Выбор значения относительного коэффициента демпфирования  осуществляется исходя из решения оптимизационной задачи, при этом в качестве критерия качества используется для ИНС морского применения обеспечение минимума дисперсий погрешностей в установившемся режиме. Известно, что если преобладающее влияние на погрешности аналога вертикали оказывают нестабильности дрейфов гироскопов, то оптимальное значение  будет равно

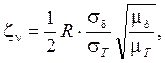 при

если шумы акселерометров, то

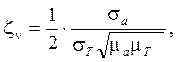 при

если локальные изменения УОЛ, то

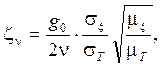 при                                                                              (9.3.21)

Так при  получим, что .

Получив таким образом оценку погрешностей аналогов вертикали и ИСК и задавшись значениями средних значений и ковариационных матриц вектора  погрешностей измерения углового положения измерительного блока БИИМ относительно объекта в соответствии с соотношениями (9.1.7) и (9.1.10) приближенно можно оценить и уровень погрешностей БИИМ на ДУС для автономного режима ее работы в выработке навигационных параметров и параметров ориентации.

Подставляя аналитические решения (9.3.10) для погрешностей аналога ИСК и решения типа (9.3.19) для погрешностей аналога вертикали в известные (Л.8) кинематические соотношения

 

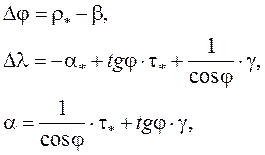
получим аналитические решения для погрешностей БИИМ в выработке навигационных параметров (координат места и курса).

9.4. Аналитические решения для погрешностей автономного режима работы БИИМ на конечном интервале времени

·  По параметрам ориентации

При разложении в степенной ряд погрешностей  БИИМ в решении задачи ориентации для автономного режима работы на конечном интервале времени  получим следующие приближенные решения:

,

,

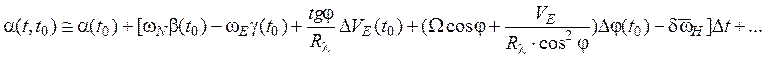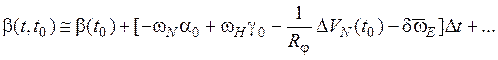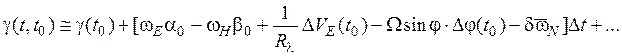,                   (9.4.1)

где

, , ;

·  По навигационным параметрам

Можно показать, что при разложении в степенной ряд погрешностей ,   БИИМ для автономного режима ее работы в выработке плановых координат на конечном интервале времени  в соответствии с моделью погрешностей БИИМ, ограничиваясь при этом полиномом третьего порядка, будем иметь

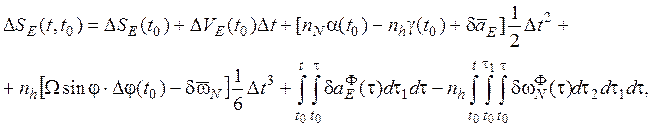
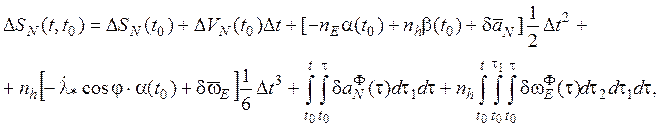            (9.4.2)

…;

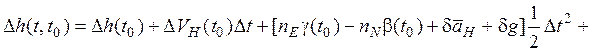где ;  - погрешности начальных условий по параметрам ориентации и навигационным параметрам, обусловленные погрешностями обсервационного режима работы ИСОН;  и  - соответственно систематические и флуктуационные составляющие погрешностей акселерометров и гироскопов ИБ БИИМ.

Приложение

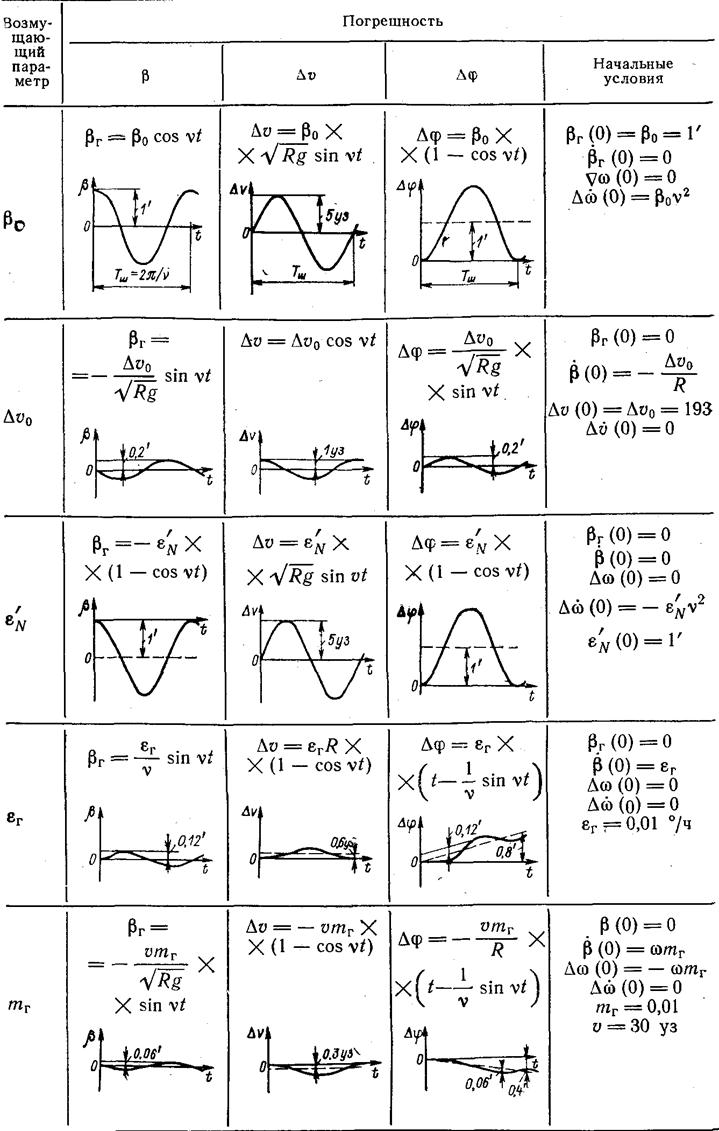
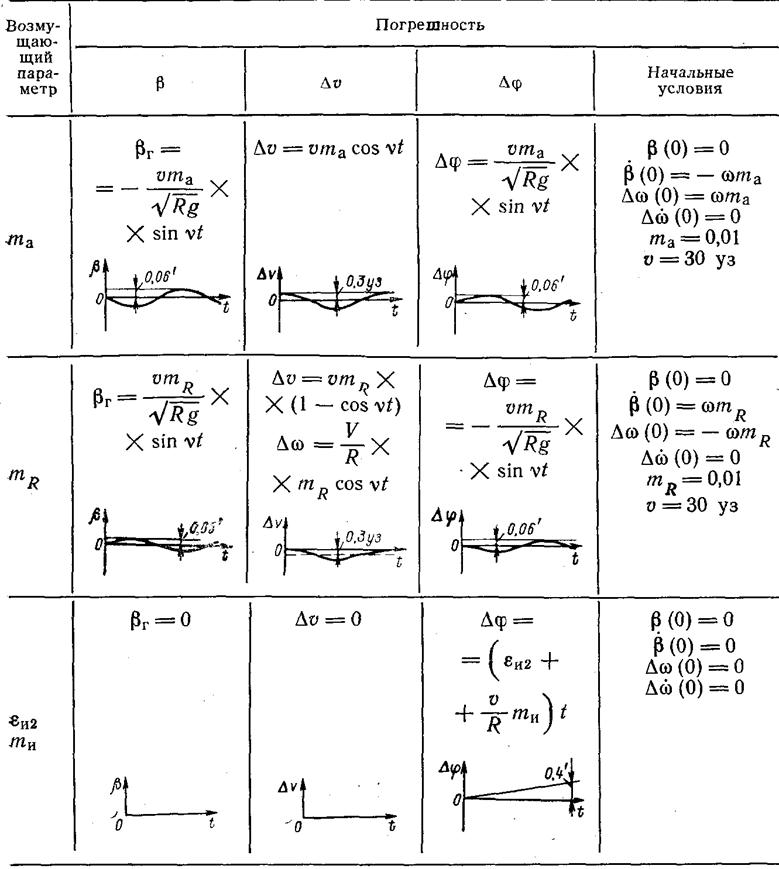
Графики процессов, протекающих в недемпфированном контуре вертикали ИИМ

В Табл.1[48] приведены результаты моделирования погрешностей недемпфированного аналога вертикали ИИМ при ненулевых начальных условиях () и входных воздействиях ступенчатого вида, где

;

 - смещение нулей соответственно акселерометра с первым интегратором, гироскопа и второго интегратора;

 - погрешности масштабов соответственно акселерометра, гироскопа, масштабирующего множителя и второго интегратора.

Примечание: В первой строке Табл.1 кривая для  справедлива при условии, что при решении задачи начальной выставки инерциального контура БИНС (в задаче ориентации) погрешность построения оси Мира в плоскости меридиана места .

Табл.1