Л.9. Анализ погрешностей бескарданных инерциальных измерительных модулей
9.1. Общие положения
Модель погрешностей БИИМ в выработке навигационных и динамических параметров в векторно-матричной форме в терминах пространства состояний согласно приведенным ранее скалярным уравнениям (см. Л8 раздела 2) может быть представлена в следующем виде:
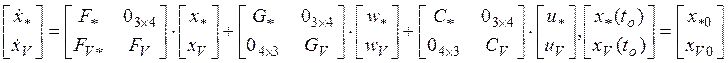
![]() (9.1.1)
(9.1.1)
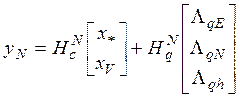 ,
, 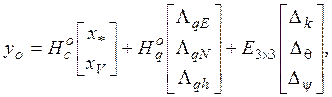
где ![]()
- векторы состояний погрешностей соответственно аналогов ИСК и вертикали места, а также вертикального канала корректируемого БИИМ;
![]() - матрицы динамики соответственно
аналогов ИСК (8.24) и вертикали места (8.38), а также вертикального канала (8.39)
БИИМ;
- матрицы динамики соответственно
аналогов ИСК (8.24) и вертикали места (8.38), а также вертикального канала (8.39)
БИИМ;
![]() - матрицы взаимосвязи соответственно
аналога вертикали с аналогом ИСК и вертикального канала с аналогом вертикали;
- матрицы взаимосвязи соответственно
аналога вертикали с аналогом ИСК и вертикального канала с аналогом вертикали;
![]() и
и ![]() -
входные возмущения и матрицы коэффициентов при входных возмущениях;
-
входные возмущения и матрицы коэффициентов при входных возмущениях;
![]() , - “нулевые” и единичная матрицы
соответствующих размеров;
, - “нулевые” и единичная матрицы
соответствующих размеров;
![]() и
и ![]() - управляющие воздействия,
соответствующие режиму работы БИИМ, и матрицы коэффициентов при данных
управлениях;
- управляющие воздействия,
соответствующие режиму работы БИИМ, и матрицы коэффициентов при данных
управлениях;
![]() ,
, ![]() -
векторы погрешностей БИИМ в выработке соответственно навигационных параметров и
параметров ориентации;
-
векторы погрешностей БИИМ в выработке соответственно навигационных параметров и
параметров ориентации;
![]() ,
,![]() и
и
![]() ,
,![]() -
матрицы связи, соответствующие кинематическим соотношениям (8.20) или (8.53) для
навигационных параметров и (8.44) или (8.65) для параметров ориентации, при
этом для БИИМ на ДУС
-
матрицы связи, соответствующие кинематическим соотношениям (8.20) или (8.53) для
навигационных параметров и (8.44) или (8.65) для параметров ориентации, при
этом для БИИМ на ДУС ![]() .
.
Погрешности БИИМ в выработке навигационных и динамических параметров, как линейной динамической системы при воздействии случайных возмущений, могут быть полностью охарактеризованы, как известно [26, 51], векторами средних значений
![]() (9.1.2)
(9.1.2)
и ковариационными матрицами
![]() (9.1.3)
(9.1.3)
где ![]() ;
;![]() -
оператор математического ожидания.
-
оператор математического ожидания.
При этом для векторов средних значений погрешностей БИИМ будут справедливы следующие решения:
 (9.1.4)
(9.1.4)
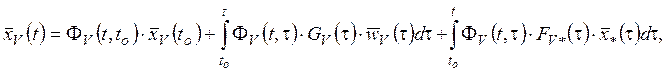 (9.1.5)
(9.1.5)
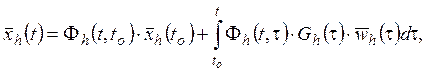 (9.1.6)
(9.1.6)
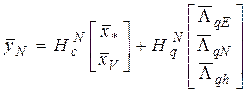 ,
,
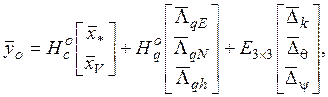 (9.1.7)
(9.1.7)
где ![]() - переходные матрицы состояния
соответственно аналогов инерциальной системы координат и вертикали места, а также
вертикального канала, которые для стационарного случая (
- переходные матрицы состояния
соответственно аналогов инерциальной системы координат и вертикали места, а также
вертикального канала, которые для стационарного случая (![]() )
равны
)
равны
![]() , (9.1.8)
, (9.1.8)
причем ![]() - единичные матрицы соответствующих
размерностей.
- единичные матрицы соответствующих
размерностей.
Решения вида (9.1.4)…(9.1.7) целесообразно использовать для описания погрешностей БИИМ, имеющих квазидетерминированный характер в одном запуске системы и обусловленных погрешностями начальной выставки или протяженной коррекции БИИМ, погрешностями калибровки коэффициентов модели дрейфов их гироскопов и акселерометров, списывающих устройств позиционных гироскопов типа ЭСГ, а также глобальными и региональными составляющими аномалий гравитационного поля (АГП) Земли, которые могут быть аппроксимированы постоянными величинами в районе движения объекта.
Анализ погрешностей БИИМ, обусловленных нестабильностью в пуске дрейфов гироскопов и погрешностей акселерометров, флуктуациями морских течений и инструментальных погрешностей лага и глубиномера или высотомера, локальными изменениями АГП и другими возмущениями, носящими случайный характер, можно проводить, исходя из следующих решений:
1) либо путем вычисления сначала корреляционных матриц погрешностей подсистем: аналогов ИСК, вертикали и вертикального канала
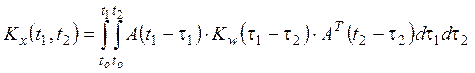 , (9.1.9)
, (9.1.9)
где ![]() весовые матрицы подсистем,
весовые матрицы подсистем, ![]() корреляционные матрицы входных
возмущений;
корреляционные матрицы входных
возмущений;
и
соответственно ковариационных матриц ![]() при
при ![]() , а затем нахождения ковариационных
матриц погрешностей БИИМ в выработке навигационных и динамических параметров
, а затем нахождения ковариационных
матриц погрешностей БИИМ в выработке навигационных и динамических параметров
![]() ,
, ![]() ,
(9.1.10)
,
(9.1.10)
где ![]() - ковариационные матрицы векторов
- ковариационные матрицы векторов ![]() ,
, ![]() ,
,
![]() ;
;
2) либо путем вычисления сразу ковариационных матриц ![]() ,
, ![]() из
решений для матриц ковариаций
из
решений для матриц ковариаций ![]() рассматриваемых
подсистем с расширенными векторами состояний
рассматриваемых
подсистем с расширенными векторами состояний ![]() ,
т.е. когда коррелированные возмущения
,
т.е. когда коррелированные возмущения ![]() описываются
марковскими процессами с входными белыми шумами интенсивности
описываются
марковскими процессами с входными белыми шумами интенсивности ![]() и вносятся в вектор состояния системы.
Эти решения
и вносятся в вектор состояния системы.
Эти решения
 (9.1.11)
(9.1.11)
соответствуют матричному дифференциальному уравнению
![]() (9.1.12)
(9.1.12)
где ![]() - соответствующие матрицы для
системы с расширенным вектором состояния.
- соответствующие матрицы для
системы с расширенным вектором состояния.
Затем уже
находим решения для ковариационных матриц ![]() погрешностей
БИИМ.
погрешностей
БИИМ.
Следует заметить, что решение вида (9.1.9) и (9.1.10) целесообразно применять при нахождении аналитических зависимостей для дисперсий погрешностей БИИМ, а решение матричного дифференциального уравнения (9.1.12) обычно используется при численном интегрировании, так как вектор состояния системы во втором случае значительно расширен из-за представления входных возмущений марковскими процессами различной размерности с входными белыми шумами.
Для анализа погрешностей БИИМ в выработке динамических параметров
используются также следующие полиномы, аппроксимирующие погрешности системы по
составляющим вектора линейной скорости или перемещения на интервале времени ![]() взаимодействия с корабельными
потребителями:
взаимодействия с корабельными
потребителями:
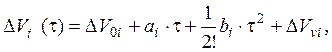 или
или
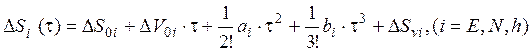 , (9.1.13)
, (9.1.13)
где ![]() ,
,![]() -
интервал времени выставки (калибровки) бортовой системы потребителя, на котором
определяются коэффициенты аппроксимирующих полиномов.
-
интервал времени выставки (калибровки) бортовой системы потребителя, на котором
определяются коэффициенты аппроксимирующих полиномов.
Для нахождения аналитических решений, определяющих погрешности БИИМ в выработке навигационных и динамических параметров, воспользуемся приближенными математическими моделями погрешностей моделирования в БИИМ аналогов инерциальной системы координат и вертикали места, которые справедливы в силу следующих допущений. Положим, что
·
для
того чтобы ошибки аналогов инерциальной системы координат и вертикали места
описывались системой стационарных линейных дифференциальных уравнений, объект
перемещается с постоянной линейной скоростью (![]() )
по параллели Земли (
)
по параллели Земли (![]() );
);
![]() ,
,
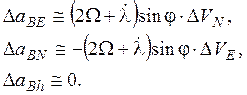 . (9.1.14)
. (9.1.14)
Модель дрейфов ДУС может быть аппроксимирована в виде суммы нескольких составляющих:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.