Линейное программирование. Задача о выборе оптимальных технологий. Задача о распределении производственной программы

Математическое программирование.

Линейное программирование.

1.  Основные понятия.

Общая задача мат. моделирования формулируется следующим образом.

Требуется найти значения n перемен. x1,x2,x3….xn, которые удовлетворяют m требованиям и неравенством

и максимизировать(минимизировать) функцию

z= f(x1,x2,…xn)    (1.2.)

Условие (1.1) называется ограничениями, а функция (1.2) – целевой

Предполагается, что функции  и f известна, bi заданные постоянные. Величины m и n между собой не связаны. Не переменные могут налагаться условия не отрицательности, цело численности.

Набор чисел x=(x1,x2,x3,….xn), удовлетворяют (1.1) называется планом задачи мат. программирования. План X задачи(1.1) и (1.2) с неотрицательными компонентами называется допустимыми. План X^*=(x1^*,x2^*,…xn^*)  доставляющий экстремум функции (1.2) называется оптимальным.

Если все функции в (1.1) и (1.2) линейны, то задача называется линейной.

А раздел математического программирования будет линейным программированием. Его методы широко применяются на промышленных предприятиях:

-  при оптимизации производственной программы

-  распределении её по цехам

-  участкам по временным интервалам

-  при ассортиментной загрузке оборудования

-  в задачах текущего и переменного,

-  технологического планирования

-  при планировании грузопотоков

-  определении плана товарооборота и его распределении

-  составлении оптимальных смесей

-  раскройно-транспортных и производственно-транспортных задач

Если хотя бы одна из функций или система ограничений изменяется во времени или целевая функция z(x) имеет оптимальную структуру

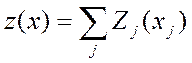
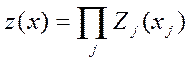
Или сам процесс принятия решений имеет многошаговый характер, то такие задачи решаются методом динамического программирования.

В управлении промышленным предприятием таким методом решаются задачи текущего и перспективного планирования.

-  управление производством

-  распределением ограниченных ресурсов

-  оптимального размещения

-  замены оборудования

Если на все или некоторые переменные Xj наложено условие дискретности, напр. Целочисленности (Xj=0,1,2….), то такой раздел программирования считается дискретным (целочисленным). К таким относятся задачи выпуска делимой продукции, маршрутами

-  управлении поставками при заданных транзитных нормах отпуска.

-  Размещение производственно-складской структуры.

2.  Некоторые модели задач линейного программирования.

2.1  Задача о выборе оптимальных технологий

Пусть для выпуска некоторой однородной продукции можно использовать n=i,n технологий. Для этого требуется m видов исходнных ресурсов, заданных b1,b2…bm

Cj-  стоимость конечной продукции (в рублях), производимой в единицу времени по j-му технологич. Способу

a_i,j – расход i-го исходног ресурса в еденицу времени по j-му технологич. способу.

В качестве неизвестной величины Xj примем время, в течение которого предприятие вырабатывает продукцию по j-му технологич. способу.

Пренебрегая временем переналадок, необходимых для перехода от одного технологич. способа к другому, получим следующ. математич. модель задачи

Максимизировать объём  выпуска продукции

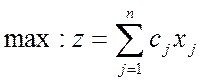   (2.1)

при ограничениях

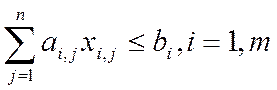  (2.2)

                      (2.3)

Пример 1

Предприятие может работать по трём технологическим способам. Расход ресурсов на единицу времени при соответствующей технологии и продолжительность представлены в таблице. Определим    использования технологического способа

Модель задачи:

Max: Z=300x₁+250x₂+450x₃

При ограничениях:

15x₁+20x₂+25x₃   1200

2x₁+3x₂+2.5x₃   150

35x₁+60x₂+60x₃   300

x_j  0         j=1.3

3.  Задача о смесях.

Критерием оптимальности можно принять минимум растрат на исходные материалы.

Построим математическую модель задачи.

Пусть a_ij – ф-ия i-го (i=1,m) химического элемента в исходном шихтовом материале j – го (j=1,n) вида. Обозначим через x_j ф-ию j-го материала, включаемого в состав шихты. Тогда содержание I – го элемента в шихте выбранного состава выразится суммой