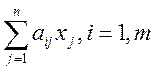
Однако в результате окислительного процесса содержание некоторых химических элементов в расплаве существенно уменьшается ( происходит их угар). В связи с этим в состав расплава следует вводить поправочный коэффициент. Если обозначить величину угара через w, то поправочный коэффициент будет равен (1-w). Вот почему фактическое содержание химических элементов в расплаве следует находить по формуле
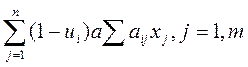
Реальная величина i-го химического элемента в расплаве должна колебаться между нижними bi и верхними Bi пределами. Обозначим через cj стоимость единицы j-го исходного материала. Модель задачи об оптимальном составе шихты принимает вид
min:z=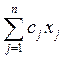 (1_
(1_
При ограничениях:
На верхний и нижний уровень содержания в расплаве химического элемента
bi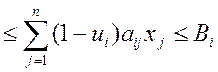 i=1,m (2)
i=1,m (2)
На комплектность долевого участка исходных материалов
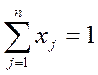 (3)
(3)
Граничные условия, определяемые технологией выплавки и ограниченностью отдельного и исходного материалов, таковы Dj j=1,n
![]()
|
Химический состав |
Исходные материалы |
Содержание химического элемента в С2,% |
Угар |
|||||
|
АК6-П-6-1 |
А1-1 |
А1-1 |
ФС-18 |
ФХ650 |
(ВС) |
|||
|
Кремний Марганец Фосфор Хром |
1,80 0,70 0,10 0 |
2,20 0,60 0,01 0 |
0,40 0,40 0,10 0 |
19,50 1,00 0,10 0 |
1,50 0,00 0,04 65,00 |
2,25 0,575 0,12 0,30 |
0,2-2,5 0,45-0,70 0-0,12 0,2-0,9 |
15 20 0 18 |
|
Граничные условия |
12 |
30 |
30 |
minZ |
||||
|
Цена, руб. |
70,8 |
40,1 |
51,00 |
78,00 |
226,0 |
56,50 |
||
|
План |
X1 |
X2 |
X3 |
X4 |
X5 |
X0 |
||
Пример: Найти оптимальный состав шихты для о граночного способа выплавки серого чугуна С2. В состав шихты в связи с коньюктурой металлорынка имеется возможность включать 6 видов исходных материалов. Необходимые сведения о содержания в них кремния, марганца, фосфора и хрома, пределы содержания в расплаве этих химических элементов, среднее содержание каждого элемента в единице шихтовых материалов, цены еденицы материалов а также потери от угара представлены в таблице. Составить математ. Модель задачи и определить оптимальный состав шихты.
Составим математическую модель задачи:
(1) min: z=70.8x1+40.1x2+51x3+78x4+226x5+56.5x6
при ограничениях на химический состав шихты:
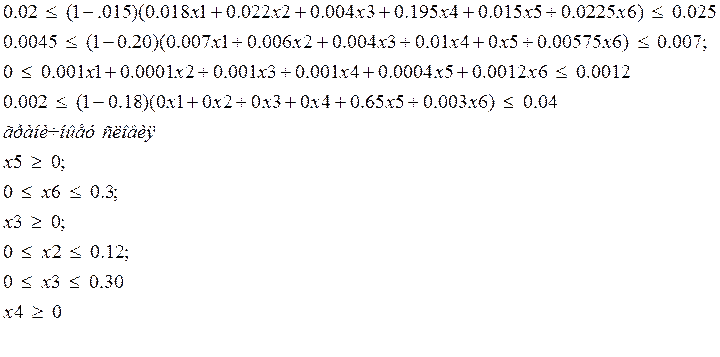
2.5 Задача о распределении производственной программы.
( о размещении заказов или загрузке взаимозаменяемых групп оборудования)
Речь идёт о задаче распределения замеров между m ( i=1,m) предприятиями ( цехами, станками, исполнителями) с различными производственными и технологическими характеристиками по взаимозаменяемых в смысле выполнения заказов. Требуется составить такой план размещения заказов ( загрузки оборудования), при котором задание было бы выполнено, а показатели эффективности достигал экстремального значения.
Сформулируем задачу математически. Пусть не m ( i=1,m) однородных группах оборудования нужно изготовить n (j = 1,n) видов продукции. План выпуска Каждого вида на определённый период задан набором xj
j = 1,n.
Мощность каждого вида оборудования ограничена и равна bi.
Известна технологическая матрица ![]() , где aij – число единиц продукции j, выпускаемой в
единицу времени на i-ом оборудовании. Пусть aij – число
единиц продукции j , выпускаемой в единицу времени на i –м
оборудовании. Пусть cij – затраты, связанные с выпуском единицы j-ой
продукции на i – ом оборудовании. Xij –
неизвестная величина – объём выпуска j – ой продукции на i –
ом оборудовании. Модель задачи примет вид: целевая функция – минимизация
расходов на реализацию всех заказов.
, где aij – число единиц продукции j, выпускаемой в
единицу времени на i-ом оборудовании. Пусть aij – число
единиц продукции j , выпускаемой в единицу времени на i –м
оборудовании. Пусть cij – затраты, связанные с выпуском единицы j-ой
продукции на i – ом оборудовании. Xij –
неизвестная величина – объём выпуска j – ой продукции на i –
ом оборудовании. Модель задачи примет вид: целевая функция – минимизация
расходов на реализацию всех заказов.
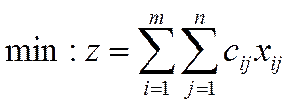 (1)
(1)
при ограничениях:
на ресурсы оборудования
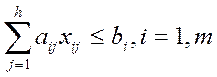 (2)
(2)
на выпуск продукции
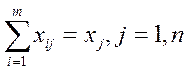 (3)
(3)
условие не отрицательности
xij![]() 0 (4)
0 (4)
Задачу (4) иногда называют распределительной. Если по некоторым видам продукции допускается превышение плана, то ограничение (3) примет вид
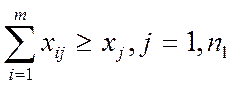
По продукции, заказы на которую принимаются по кооперации для более полной загрузки оборудования, ограничения можно записывать так:
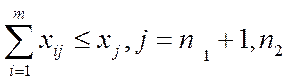
Для продукции, выпуск которой g:
Соответствовать плану, ограничения таковы
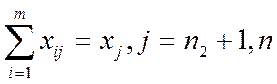
В качестве целевой функции можно принять:
Максимум прибыли
Max: 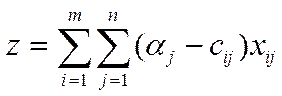
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.