Линейное программирование. Задача о выборе оптимальных технологий. Задача о распределении производственной программы, страница 4

x₁₁+x₂₁+x₃₁=3x

x₁₂+x₂₂+x₃₂=2

x₁₃+x₂₃+x₃₃=2x

x₁₄+x₂₄+x₃₄=4x

x₁₅+x₂₅+x₃₅=3x

2.5 Задача загрузки не взаимозаменяемых групп оборудования.

Пусть имеется m(i=1,m) групп оборудования, на котором нужно выпускать n (j=1,n) видов продукции. Предполагается, что группы оборудования различны. В пределах данной технологии одна и та же продукция на другом оборудовании не производится, т.е. оборудование взаимно заменяется лишь при замене технологического способа  производства.

Пусть k (k=1,k) – номер технологич. способа. Обозначим через a_ij^k норму затрат времени на обработку единицы j-ой продукции на i-ом оборудовании по всему технологическому способу. Пусть b_i – общий полезный фонд времени работы i-ой группы оборудования.

Неизвестная величина задачи x_jk – объём продукции j-го вида, вырабатываемой по k-ой технологии; x_j – заданный сверху план j- ой продукции; c_jk – затраты связанные с изготовлением единицы j – ой продукции по всей технологии, которые следует минимизировать.

Матеем. модель задачи

minz=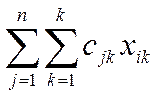   (1)

при ограничениях :

- по фону времени работы каждой группы оборудования

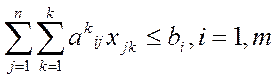    (2)

- на выпуск продукции

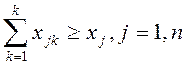   (3)

- Условие не отрицательности x_jk  (4)

Пример.

Имеется три группы оборудования, фрезерные станки, токарные станки, сварочные аппараты. С его помощью выпускается 3 вида продукции: клапаны, распределительные валы и зубчатые колёса. Разработано 3 технологии. Нормативные коэффициенты a_ij^k, фонд времени b_i и прибыль c_jk, полученная от реализации единицы j-ой продукции произведённой по k-ой технологии предст. в табл.. Необходимо определить план выпуска x_jk каждого вида продукции (j=1,3) ( используя каждую технологию (k=1,3)), доставляющий предприятию максимум прибыли.

Модель задачи:

Целевая функция – max прибыли.

max:z=12x₁₁+8x₁₂+7x₁₃+10x₂₁+8x₂₂+11x₂₃+18x₃₁+15x₃₂+16x₃₃

При ограничениях: на фонд времени работы каждой группы оборудования( для фрезерных станков)

1.5x₁₁+2x₁₂+x₁₃+2.5x₂₁+0.5x₂₂+3x₂₃+3x₃₁+2x₃₂+2.5x₃₃25

для токарных станков

3x₁₁+x₁₂+2.5x₁₃+1.5x₂₁+2.5x₂₂+0.5x₂₃+5x₃₁+6x₃₂+4x₃₃40

для сварочных аппаратов

0,5x₁₁+4x₁₂+3x₁₃+x₂₁+3x₂₂+x₂₃+4x₃₁+7x₃₂+8x₃₃50

условие не отрицательности x_ij

 

Группы оборудования	Выпускаемая продукция									Фонд времени работы оборуд.
	Клапаны			Валы			Зубчатые колёса
	k-1	k-2	k-3	k-1	k-2	k-3	k-1	k-2	k-3
Фрезерные станки	1,5	2	1	2,5	0,5	3	3	2	2,5	25
Токарные станки	3	1	2,5	1,5	2,5	0,5	5	6	4	40
Сварочные аппараты	0,5	4	3	2	3	5	4	8	7	50
Прибыль, тыс. руб	12	8	7	10	8	11	18	15	10	Maxz
Интенсивность использования способа	X11	X12	X13	X21	X22	X23	X31	X32	X33

Рассмотрим на конкретном примере основные этапы решения задачи линейного программирования симплекс-методом. Пусть некоторое предприятие м. изготовляет изделия 4-х видов n1,n2,n3,n4. Известно что для изготовления изделия требуется 3 вида оборудования: О1,О2,О3. Известно также сколько времени потребуется на изготовление изделия на оборудовании, фонд времени оборудования и сколько прибыли м.б. получено при реализации изделия по оборудованиям, чтобы предприятие имело бы максимальную прибыль

ОI	Uj				bi
	U1	U2	U3	U4
O1	a11=3	a12=5	a13=2	a14=7	b1=15
O2	a21=4	a22=3	a23=3	a24=5	b2=9
O3	a31=5	a32=6	a33=4	a34=8	b3=30
CJ	c1=40	c2=50	c3=30	c4=20

Обозначим: b_i= ресурсы оборудования o_i

a_ij – время изготовления j-го изделия u_j на i-ом оборудовании

c_j – прибыль от  одного изделия U_j

x_j -  количество j-х изделий, которое необходимо выпускать на предприятии.

Решение:

Составим математическую модель задачи

max: z=40x₁+50x₂+30x₃+20x₁

3x₁+5x₂+2x₃+7x₄

4x₁+3x₂+3x₃+5x₄ 9

5x₁+6x₂+4x₃+8x₄30

x₁0_, x₂0_, x₃0_, x₄0