Линейное программирование. Задача о выборе оптимальных технологий. Задача о распределении производственной программы, страница 3

Где - отпускная цена единицы j-ой продукции;

Минимум затрат станочного времени

Min: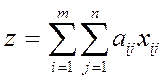

Выполнение задания в минимальные сроки

Min: z=max{t_i}, где t_i= 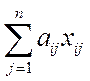 и др.

Математическая модель задачи о распределении производственной программы в случае выпуска комплексной продукции примет вид (x – число комплектов, a_ij – число единиц j-ой продукции, входящей в комплект)

Max: Z=x  (5)

При ограничениях:

На ресурсы оборудования

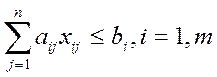  (6)

на комплектность продукции

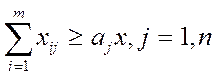  (7)

Условие не отрицательности

(8)

Пример.  В цехе имеются три группы взаимно заменяемого оборудования с мощностями до 400, 850, 300 норма часов в месяц. Цеху дан план выпуска пяти видов продукции соответственно в объёмах П1-600 единиц, П2-350, П3-450, П5-600. Время изготовления единицы каждого вида продукции на одном оборудовании составляет 0.8,0.6,0.4,0.8,0.5 часа, на втором – 0.6;0.8;0.7;1.2;0.9; на третьем – 1.4;0.5;0.9;0.6 и 1.0. Затраты на изготовление единицы продукции на первом оборудовании равна 20,10,40,50 и 80; на втором – 50,40,40,30 и 60; на третьем – 65,90,30,20 и 50. Отпускная цена единицы каждой продукции 80,100,60,50 и 85 руб.

Составить план размещения заказов,  корректирующий выполнение задания a: а) доставляющий максимум прибыли;

б) минимизирующий общую стоимость изготовления продукции;

в) минимизирующий затраты станочного времени работы оборудования;

г) минимизирующий время работы оборудования, т.е. регулируемый в минимальные сроки;

д) обеспечивающий выпуск максимального числа комплектов, каждый из которых включает 3 изделия П1, одно П2, два изделия П3, 4 изделия П4 и 3 изделия П5. Условия задачи для удобства сведены в таблицу.

Группа оборудования	Выпускаемая продукция					Объём ресурсов В норма часах
	П1	П2	П3	П4	П5
1	20 0,3 x11	10 0,6 x12	40 0,4 x13	50 0,8 x14	80 0,5 x15	400
2	50 0,6 x21	40 0,8 x22	40 0,7 x23	30 1,2 x24	60 0,9 x25	850
3	65 1.4 x31	90 0,5 x32	30 0,9 x33	20 0,6 x34	50 1,0 x35	300
Задание по выпуску	600	350	450	500	600	maxZ1
Отпускная цена	80	100	60	50	85	minZ2 minZ3
Комплект	3	1	2	4	3	maxZ2

Математическая модель задачи:

а) целевая функция – max прибыли

max: z₁=(80-20)x₁₁+(100-10)x1₂+(60-40)x₁₃+(50-50)x₁₄+(85-80)x₁₅+(80-50)x₂₁+(100-40)x₂₂+(60-40)x₂₃+(50-30)x₂₄+(85-60)x₂₅+(80-65)x₃₁+(100-90)x₃₂+(60-30)x₃₃+(50-20)x₃₄+(85-50)x₃₅

При ограничениях:

на ресурсы оборудования

0,3x₁₁+0,6x₁₂+0,4x₁₃+0,8x₁₄+0,5x₁₅

0,6x₂₁+0,8x₂₂+0,7x₂₃+1,2x₂₄+0,5x₂₅

1,4x₃₁+0,5x₃₂+0,9x₃₃+0,6x₃₄ +1x₃₅

на объёмы выпуска продукции

x₁₁+x₂₁+x₃₁=600

x₁₂+x₂₂+x₃₂=450

x₁₄+x₂₄+x₃₄=500

x₁₅+x₂₅+x₃₅=300

Усилие неотрицательных x_ij 0

б) Целевая функция – минимум стоимости изготовления продукции:

min: z₂=20x₁₁+10x₁₂+40x₁₃+50x₁₄+80x₁₅+50x₂₁+40x₂₂+40x₂₃+30x₂₄+60x₂₅+65x₃₁+90x₃₂+30x₃₃+20x₃₄+50x₅

Ограничения те же, что и в а)

в) Целевая функция – минимум станочного времени работы оборудования:

min: z₃=0.3x₁₁+0.6x₁₂+0.4x₂₄+0.8x₁₄+0.5x₁₅+0.6x₂₁+0.8x₂₂+0.7x₂₃+1.2x₂₄+0.9x₂₅+1.4x₃₁+0.5x₃₂+0.9x₃₃+0.6x₃₄+1x₅₅

 

Ограничения те же, что и в а).

г) Функция цели – минимальное время реализации всего оборудования. Обозначим t1,t2,t3 время работы 1,2,3 групп оборудования.

Получим

t1=0.3x₁₁+0.6x₁₂+0.4x₁₃+0.8x₁₄+0.5x₁₅

t2=0.26x₂₁+0.8x₂₂+0.7x₂₃+1.2x₂₄+0.9x₂₅

t3=1.4x₃₁+0.5x₃₂+0.9x₃₃+0.6x₃₄+1.0x₃₅

Поскольку все группы оборудования работают одновременно, то время (t) реализации планового задания равно наибольшему из них:

t=max{t1,t2,t3}

Отсюда модель задачи примет вид

minz=max{t_i}

при ограничениях на объём выпуска продукции и условие не отрицательности.

Это задача с так называемым мини-макс. критерием. Она легко сводится к задаче линейного программирования.

В самом деле 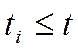 Имеем : minz=t

при ограничениях:

x₁₁+x₂₁+x₃₁=600

x₁₂+x₂₂+x₃₂=350

x₁₃+x₂₃+x₃₃=450

x₁₄+x₂₄+x₃₄=500

x₁₅+x₂₅+x₃₅=300

0.3x₁₁+0.6x₁₂+0.3x₁₃+0.8x₁₄+0.5x₁₅

0.6x₂₇+0.8x₂₂+0.7x₂₃+1.2x₂₄+0.3x₂₅

1.4x₃₁+0.5x₃₂+0.9x₃₃+0.6x₄+1.0x₃₅

x_ij ,

 

д) Целевая функция – максимизирующая числа компонентов x.

Модель задачи maxz=x при ограничениях на ресурсы оборудования – что и в случае а);