В задаче дано:
1) расчетная схема стержня (в РГР-2 принять расчетную схему задачи №1 из РГР-1);
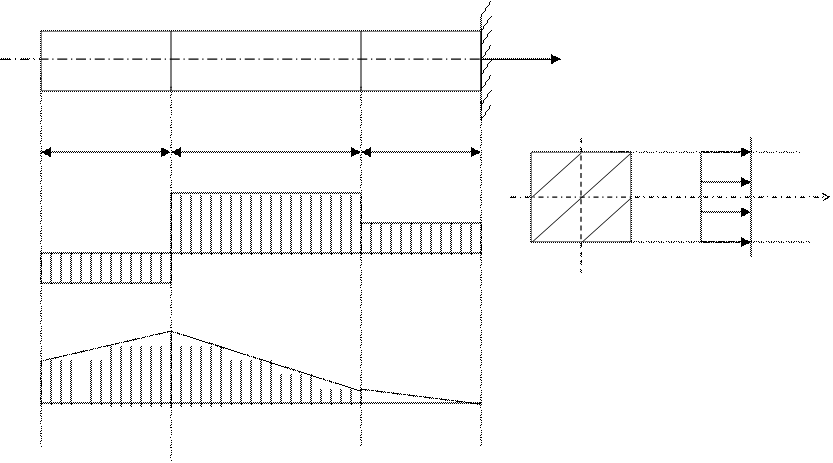
2) эпюра продольных сил Nx (построена при выполнении РГР-1);
3) допускаемое напряжение на растяжение и сжатие для материала стержня [σl] = 150 МПа;
4) модуль продольной упругости материала стержня E = 2*105 МПа;
5) допускаемое
перемещение стержня ![]() ;
;
Требуется:
1) для стержня постоянного поперечного сечения определить размеры сечения, приняв его форму в виде квадрата;
2) определить нормальные напряжения σ в одном из опасных сечений стержня и построить эпюру распределения этих напряжений по высоте сечения;
3) определить осевые перемещения сечений стержня, построить эпюру перемещении ∆l и проверить стержень на жесткость;
4) если условие жесткости (1.2) не выполняется, определить новые размеры поперечного сечения стержня на основе условия (1.2);
Решение:
 |
![]()
По эпюре продольных сил Nx определяется опасное сечение стержня и максимальная по абсолютной величине продольная сила |Nxmax| в нем.
Из условия (1.1) определяется требуемая площадь поперечного сечения стержня:
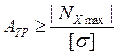 (1.1);
(1.1); 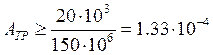 ;
;
Находятся требуемые и
окончательные размеры поперечного сечения стержня постоянного сечения в виде
квадрата: ![]() , где атр
- сторона квадрата, требуемая из условия прочности:
, где атр
- сторона квадрата, требуемая из условия прочности: ![]() ;
;
A = a2, где a = 12 мм;
A = 122 = 144 мм2;
Значение σ определяется по формуле:
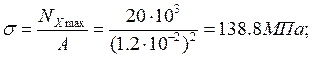
Знак напряжения σ соответствует знаку продольной силы на эпюре Nx.
При этом перемещение ∆lxi на i-ом участке равно:
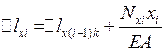 ;
;
где ∆lx(i-1)k - перемещение крайнего сечения i -1 грузового участка на границе с i - ым участком (расчет значения ∆lx(i-1)k предшествует расчету i-того участка) при расчете первого грузового участка ∆lx(i-1)k = 0); xi - координата произвольного сечения на i-том участке относительно его начала (рис. 2). Знак силы Nxi в формуле должен соответствовать знаку усилия Nxi па эпюре продольных сил.
![]() ;
;
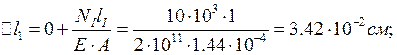
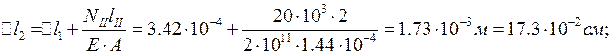
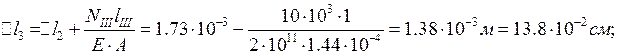
2. Расчёт стержня на прочность и жёсткость при кручении (задача №2)
В задаче даны:
1) расчетная схема стержня (в РГР-2 принять расчетную схему задачи 2 из РГР-1);
2) эпюра крутящих моментов Тх (построена при выполнении РГР-1);
3) допускаемое касательное напряжение материала стержня [τ] =90 МПа;
4) модуль сдвига материала стержня G = 8*104 МПа;
5) допускаемый угол закручивания на единицу длины стержня [Ф] = 1,2*10-2 рад/м.
Требуется:
1) из условия прочности определить диаметр стержня d сплошного поперечного сечения;
2) из условия прочности определить наружный dН и внутренний dВ диаметры стержня кольцевого поперечного сечения при a = dВ/dН=0,8;
3) сравнить по весу стержни сплошного и кольцевого поперечных сечений и оценить экономию материала при изготовлении стержня кольцевого сечения;
4) построить эпюры распределения касательных напряжений вдоль диаметра одного из опасных сечений сплошного и полого стержней;
5) определить углы закручивания сечений стержня сплошного поперечного сечения, построить эпюру углов закручивания φ и проверить стержень на жесткость;
6) если условие жесткости не выполняется, определить новый диаметр стержня сплошного сечения на основе условия жесткости.

Решение:
По эпюре крутящих моментов Тх определяется опасное сечение стержня и величина крутящего момента в нем |Txmax|.
Из условия (2.1) определяется требуемый момент сопротивления WP TP:
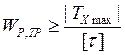 (2.1);
(2.1); 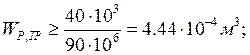
![]()
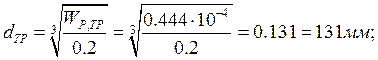
d ≥ dTP; d = 140 мм;
![]()
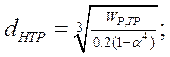
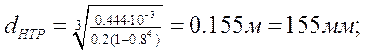
dH = 160 мм
![]()
dB = αdH; dB = 0.8 * 160 = 128 мм;
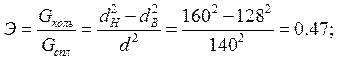
По полученному численному значению коэффициента экономичности Э делается вывод о достоинствах стержня кольцевого поперечного сечения по сравнению со сплошным.
Распределение напряжений τ при кручении в опасном сечении подчиняется закону:
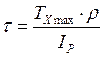 , где ρ — расстояние от
центра сечения до рассматриваемой точки; lP
— полярный момент инерции поперечного сечения стержня.
, где ρ — расстояние от
центра сечения до рассматриваемой точки; lP
— полярный момент инерции поперечного сечения стержня.
Для сечения в виде круга диаметром d:
![]()
![]()
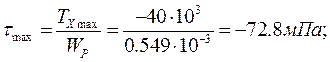
Для сечения в виде кольца:
![]()
![]()
![]()
Углы закручивания φxi на i-том участке определяются по формуле:
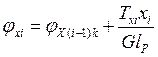 , где φx(i-1)k - угол
закручивания крайнего сечения i -1 грузового
участка, примыкающего к участку i. Расчет участка i -1 предшествует расчету участка i,
поэтому величину φx(i-1)k можно считать известной; для первого грузового
участка φx(i-1)k = 0; Txi - крутящий момент на i-том
участке; xi - координата произвольного
сечения 1-го участка относительно его начала (по аналогии с задачей № 1). Знак
момента Txi в формуле соответствует знаку Txi на эпюре крутящих моментов Тх.
, где φx(i-1)k - угол
закручивания крайнего сечения i -1 грузового
участка, примыкающего к участку i. Расчет участка i -1 предшествует расчету участка i,
поэтому величину φx(i-1)k можно считать известной; для первого грузового
участка φx(i-1)k = 0; Txi - крутящий момент на i-том
участке; xi - координата произвольного
сечения 1-го участка относительно его начала (по аналогии с задачей № 1). Знак
момента Txi в формуле соответствует знаку Txi на эпюре крутящих моментов Тх.
![]()
φ0 = 0
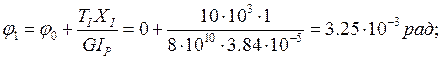
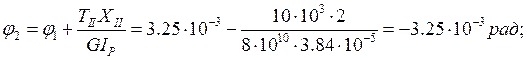
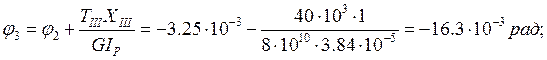
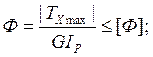
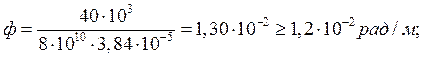
Так как условие не выполняется, необходимо найти новый момент инерции IP,TP:
![]()
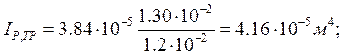
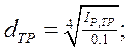
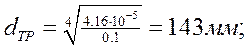
В задаче даны:
1) расчетная схема балки (задача № 3 на плоский поперечный изгиб в РГР-1);
2) эпюры поперечных сил и изгибающих моментов, построенные в РГР-1 для заданной расчетной схемы;
3) допускаемые нормальные [σ] и касательные напряжения [τ] материала балки: [σ] = 160 МПа, [τ] = 100 МПа;
4} модуль упругости материала балки Е = 2*105 МПа;
Требуется:
1) из условия прочности определить размеры прямоугольного поперечного сечения балки при h/b = 2 (h и b — соответственно высота и ширина сечения);
2) подобрать по сортаменту прокатной стали номер двутавра, удовлетворяющий, условию прочности;
3) сравнить по весу балки, прямоугольного и двутаврового поперечного сечений и определить экономию материала при изготовлении двутавровой балки;
4) для каждой из двух балок построить эпюры распределения нормальных напряжений σ по высоте опасного сечения, где Mх= |Мхmаx|;
5) для каждой из двух сечений балок построить эпюры распределения касательных напряжений τ по высоте опасного сечения, в котором Qx= |QXmax|;
6) проверить прочность балок по касательным напряжениям;
7) построить эпюры углов, поворота θ и прогибов у для двутавровой балки;
Решение:
 |
Из эпюры Мх определяется максимальное значение изгибающего момента МXmax.
Из условия (3.1) определяется требуемый момент сопротивления:
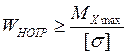 (3.11);
(3.11);
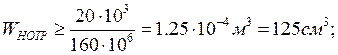
h = 2b; h = 2*60 = 120 мм;
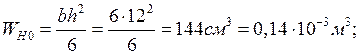
По сортаменту прокатной стали и найденному по формуле значению WН.Отр определяется номер двутавра, удовлетворяющий условию прочности. Для этого по сортаменту должен быть принят двутавр с большим ближайшим значением WНо ст (по сортаменту Wz) по сравнению с требуемым значением WHотр:
Номер двутавра: №18
WHOCT = 143 см3 = 0,143 *10 -3 м3;
WHOCT ≥ WHOTP; 143 ≥ 125 см3;
hCT = 180 мм;
bCT = 90 мм;
S = 5.1 мм;
t = 8.1 мм;
ACT = 23.4 см2;
IZ = 1290 см4;
SZ = 81.4 см3;
 |
Распределение напряжений σ в опасном сечении при изгибе подчиняется закону:
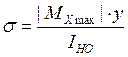 , где у -
расстояние от рассматриваемой точки до нейтральной оси сечения; IН.О - момент инерции поперечного сечения балки
относительно нейтральной оси.
, где у -
расстояние от рассматриваемой точки до нейтральной оси сечения; IН.О - момент инерции поперечного сечения балки
относительно нейтральной оси.
Для балки прямоугольного сечения:
![]()
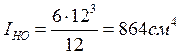 ;
;
Для двутавра:
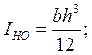
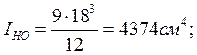
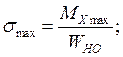 или
или
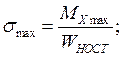
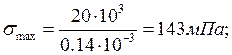
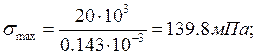
Балка прямоугольного сечения:
По эпюре поперечных сил Qx определяется максимальное по абсолютной величине значение QXmax
Распределение напряжений τ в прямоугольном сечении подчиняется закону:
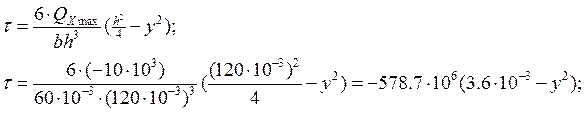
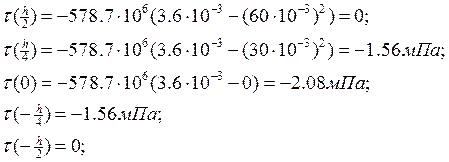
Двутавровая балка:
Напряжения τ определяются в отдельных слоях сечения по формуле Журавского:
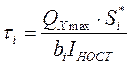 , где bi - ширина рассматриваемого слоя i; Si* - статический момент относительно
нейтральной оси части сечения, расположенный по одну сторону от
рассматриваемого слоя i. Всего рассматривается семь
слоев:
, где bi - ширина рассматриваемого слоя i; Si* - статический момент относительно
нейтральной оси части сечения, расположенный по одну сторону от
рассматриваемого слоя i. Всего рассматривается семь
слоев:
b1 = b2 = b6 = b7 = bCT; b3 = b4 = b5 = S; S1* = S7* = 0;
Для слоёв 2,3,5 и 6 моменты определяются по формуле:
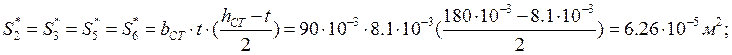
τ1 = τ7 = 0;
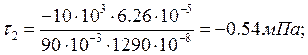
τ2 = τ6;
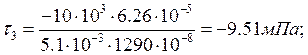
τ3 = τ5;
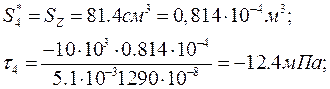
E = 2*105 мПа; двутавр №18
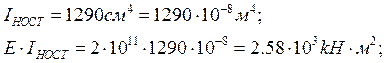
По формуле определяем углы поворота сечений:
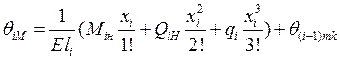 ;
;
Iгрузовой участок: 0 ≤ x1 ≤ 1;
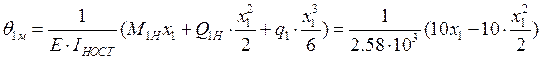 ;
;
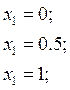
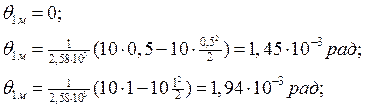
IIгрузовой участок: 0 ≤ x2 ≤ 2;
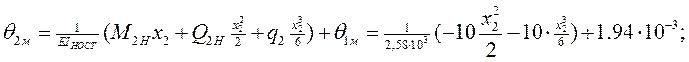
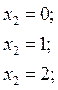
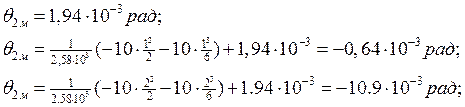
Определим прогибы yiм:
I грузовой участок: 0 ≤ x1 ≤ 1;
![]()
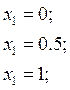
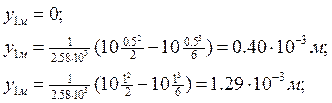
II грузовой участок: 0 ≤ x2 ≤ 2;
![]()
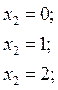
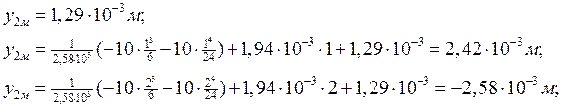
Список литературы
1. Внутренние силовые факторы в элементах химического оборудования: Метод. указания/Сост. А. М. Василенко, А. И. Мильченко; ЛТИ им. Ленсовета. Л., 1985. 34 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.