1. Вычислить коэффициент корреляции ![]() между
переменными x и y по данным
таблицы для своего варианта. Рассчитать коэффициент регрессии для линейной
модели методом наименьших квадратов.
между
переменными x и y по данным
таблицы для своего варианта. Рассчитать коэффициент регрессии для линейной
модели методом наименьших квадратов.
Таблица 1 –экспериментальные данные
|
x |
y |
x2 |
y2 |
xy |
x3 |
x4 |
yx2 |
|
3 |
21 |
9 |
441 |
63 |
27 |
81 |
189 |
|
3 |
20,9 |
9 |
436,81 |
62,7 |
27 |
81 |
188,1 |
|
3 |
21 |
9 |
441 |
63 |
27 |
81 |
189 |
|
3,3 |
23,5 |
10,89 |
552,25 |
77,55 |
35,937 |
118,5921 |
255,915 |
|
3,3 |
23,6 |
10,89 |
556,96 |
77,88 |
35,937 |
118,5921 |
257,004 |
|
3,3 |
23,7 |
10,89 |
561,69 |
78,21 |
35,937 |
118,5921 |
258,093 |
|
3,6 |
29,2 |
12,96 |
852,64 |
105,12 |
46,656 |
167,9616 |
378,432 |
|
3,6 |
29,2 |
12,96 |
852,64 |
105,12 |
46,656 |
167,9616 |
378,432 |
|
3,6 |
29,5 |
12,96 |
870,25 |
106,2 |
46,656 |
167,9616 |
382,32 |
|
3,9 |
33 |
15,21 |
1089 |
128,7 |
59,319 |
231,3441 |
501,93 |
|
3,9 |
32,5 |
15,21 |
1056,25 |
126,75 |
59,319 |
231,3441 |
494,325 |
|
3,9 |
32,6 |
15,21 |
1062,76 |
127,14 |
59,319 |
231,3441 |
495,846 |
|
4,2 |
38,5 |
17,64 |
1482,25 |
161,7 |
74,088 |
311,1696 |
679,14 |
|
4,2 |
38,4 |
17,64 |
1474,56 |
161,28 |
74,088 |
311,1696 |
677,376 |
|
4,2 |
38,3 |
17,64 |
1466,89 |
160,86 |
74,088 |
311,1696 |
675,612 |
|
4,5 |
47,7 |
20,25 |
2275,29 |
214,65 |
91,125 |
410,0625 |
965,925 |
|
4,5 |
48 |
20,25 |
2304 |
216 |
91,125 |
410,0625 |
972 |
|
4,5 |
47,7 |
20,25 |
2275,29 |
214,65 |
91,125 |
410,0625 |
965,925 |
|
4,8 |
55,3 |
23,04 |
3058,09 |
265,44 |
110,592 |
530,8416 |
1274,112 |
|
4,8 |
54,8 |
23,04 |
3003,04 |
263,04 |
110,592 |
530,8416 |
1262,592 |
|
4,8 |
54,9 |
23,04 |
3014,01 |
263,52 |
110,592 |
530,8416 |
1264,896 |
|
5,1 |
66,4 |
26,01 |
4408,96 |
338,64 |
132,651 |
676,5201 |
1727,064 |
|
5,1 |
66,7 |
26,01 |
4448,89 |
340,17 |
132,651 |
676,5201 |
1734,867 |
|
5,1 |
66,7 |
26,01 |
4448,89 |
340,17 |
132,651 |
676,5201 |
1734,867 |
|
5,4 |
77 |
29,16 |
5929 |
415,8 |
157,464 |
850,3056 |
2245,32 |
|
5,4 |
77,5 |
29,16 |
6006,25 |
418,5 |
157,464 |
850,3056 |
2259,9 |
|
5,4 |
77,1 |
29,16 |
5944,41 |
416,34 |
157,464 |
850,3056 |
2248,236 |
|
5,7 |
91,7 |
32,49 |
8408,89 |
522,69 |
185,193 |
1055,6 |
2979,333 |
|
5,7 |
92,2 |
32,49 |
8500,84 |
525,54 |
185,193 |
1055,6 |
2995,578 |
|
5,7 |
92,1 |
32,49 |
8482,41 |
524,97 |
185,193 |
1055,6 |
2992,329 |
|
130,5 |
1450,7 |
17030,25 |
2104530 |
189316,4 |
2222448 |
2,9E+08 |
24705784 |
Коэффициент корреляции определим исходя из формулы:
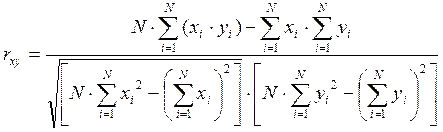 ,
,
где N=30.
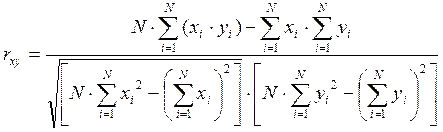 =
=
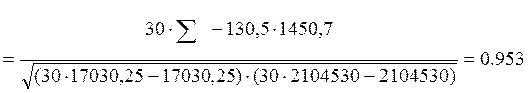
Так как коэффициент корреляции равен 0.953, то можно сделать вывод – теснота связи достаточно хорошая.
Коэффициенты регрессии для линейной модели определяются по формулам:
![]() ,
,
где x и y –средние значения.
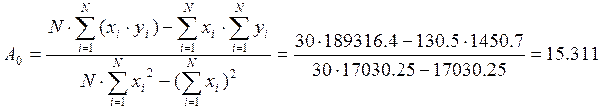
![]()
Диаграммы средней и линейной зависимостей представлены на рисунке 1.
2. Подобрать империческую формулу методом средних квадратов по
экспериментальным данным, приведенным в таблице 1, для нелинейной модели вида ![]() .
.
При расчете методом средних квадратов необходимо учитывать усредненный результат измерений, исходя из этого данные для расчета приведены в таблице 2.
Таблица 2 – Данные для расчета
|
х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
y |
60.6 |
66.3 |
76.6 |
85.6 |
100.6 |
116 |
142 |
166.6 |
203.6 |
257.6 |
Существует ошибка. Но при расчете методом средних квадратов эта ошибка равна нулю. Таким образом уравнение имеет вид:
![]()
где Е - ошибка
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Так как ошибка равна нулю, уравнение примет вид:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Разобьем уравнения на системы уравнений, составим матрицу систем и определим коэффициенты.
![]()
![]()
![]()
Диограмма приведена на рисунке 2.
3. Подобрать империческую формулу с использованием наименьших квадратов по результатам экспериментальных данных, приведенных в таблице 1, для нелинейной модели аналогично п.2.
![]()
![]()
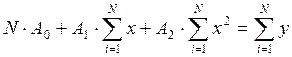
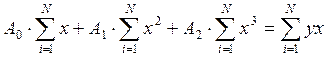
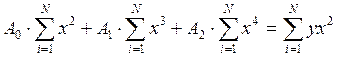
![]()
![]()
![]()
Составим матрицу систем и определим коэффициенты.
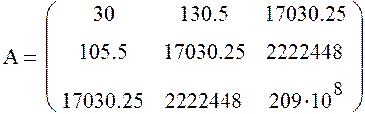
![]()
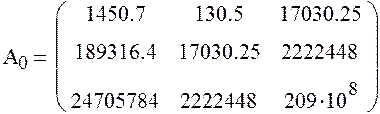
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.