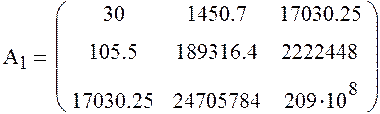
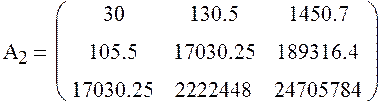
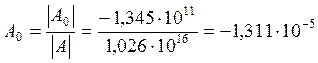
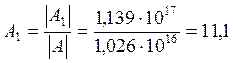
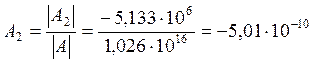
Другие предметы \ Введение в специальность

Расчёт коэффициента регрессии для линейной модели методом наименьших квадратов. Подбор имперической формулы методом средних квадратов и с использованием наименьших квадратов по экспериментальным данным, страница 2

                

               

Диаграмма приведена на рисунке 3.

4. Изобразить на графике и сравнить экспериментальные зависимости и зависимости полученные теоретически. Произвести оценку адекватности полученных теоретических выражений экспериментальным данным для значения доверительной вероятности .

Оценка адекватности с использованием критерия Фитнера.

Оценка для линейной модели вида:

Таблица 2 –Данные необходимые для расчета

x

y1

y2

y3

yiэ(ср)

yiт

yiт-yiэ(ср)

yiт-yiэ(ср)2

 ср.(yiт-yэ)2

3

21

20,9

21

20,96

233,4374

212,4774

45146,65

135431,4

3,3

23,5

23,6

23,7

23,6

263,4506

239,8506

57528,31

172585

3,6

29,2

29,2

29,5

29,3

327,9234

298,6234

89175,94

267527,9

3,9

33

32,5

32,6

32,7

362,383

329,683

108690,9

326072,8

4,2

38,5

38,4

38,3

38,4

425,7442

387,3442

150035,5

450106,6

4,5

47,7

48

47,7

47,8

530,2346

482,4346

232743,1

698229,5

4,8

55,3

54,8

54,9

55

610,2698

555,2698

308324,6

924973,8

5,1

66,4

66,7

66,7

66,6

741,4386

674,8386

455407,1

1366221

5,4

77

77,5

77,1

77,2

857,045

779,845

608158,2

1824475

5,7

91,7

92,2

92,1

92

1023,785

931,785

868223,3

2604670

сумма

4892,152

8770293

Найдем экспериментальный коэффициент Фитнера и сравним его с теоретическим.

Коэффициент Фитнера определим по формуле:

,

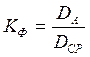где  -дисперсия адекватности;

 -средняя дисперсия.

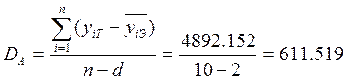
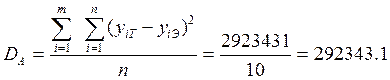
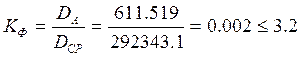
Оценка адекватности для нелинейной модели вида:

Таблица 3 –Данные необходимые для расчета

x

y1

y2

y3

yiэ(ср)

yiт

yiт-yiэ(ср)

yiт-yiэ(ср)2

 ср.(yiт-yэ)2

3

21

20,9

21

20,96

17,115

-3,845

14,78403

14,83756

3,3

23,5

23,6

23,7

23,6

24,29985

0,69985

0,48979

0,496457

3,6

29,2

29,2

29,5

29,3

31,509

2,209

4,879681

4,899681

3,9

33

32,5

32,6

32,7

38,74245

6,04245

36,5112

36,55787

4,2

38,5

38,4

38,3

38,4

46,0002

7,6002

57,76304

57,76971

4,5

47,7

48

47,7

47,8

53,28225

5,48225

30,05507

30,07507

4,8

55,3

54,8

54,9

55

60,5886

5,5886

31,23245

31,27912

5,1

66,4

66,7

66,7

66,6

67,91925

1,31925

1,740421

1,760421

5,4

77

77,5

77,1

77,2

75,2742

-1,9258

3,708706

3,755372

5,7

91,7

92,2

92,1

92

82,65345

-9,34655

87,358

87,40466

13,82425

268,8359

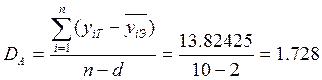
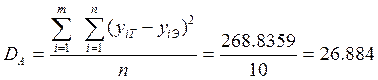
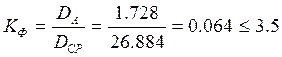
Оценка адекватности для нелинейной модели вида:

Таблица 4 –Данные необходимые для расчета

x

y1

y2

y3

yiэ(ср)

yiт

yiт-yiэ(ср)

yiт-yiэ(ср)2

 ср.(yiт-yэ)2

3

21

20,9

21

20,96

33,29999

12,33999

152,2753

152,113

3,3

23,5

23,6

23,7

23,6

36,62999

13,02999

169,7806

169,7872

3,6

29,2

29,2

29,5

29,3

39,95999

10,65999

113,6353

113,6553

3,9

33

32,5

32,6

32,7

43,28999

10,58999

112,1478

112,1945

4,2

38,5

38,4

38,3

38,4

46,61999

8,219987

67,56818

67,57485

4,5

47,7

48

47,7

47,8

49,94999

2,149987

4,622444

4,642444

4,8

55,3

54,8

54,9

55

53,27999

-1,72001

2,958445

3,005112

5,1

66,4

66,7

66,7

66,6

56,60999

-9,99001

99,80036

99,82036

5,4

77

77,5

77,1

77,2

59,93999

-17,26

297,9081

297,9547

5,7

91,7

92,2

92,1

92

63,26999

-28,73

825,4137

825,4603

-0,71013

1846,208

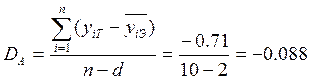
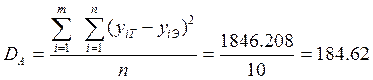
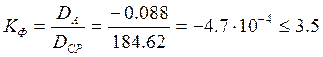
Результаты семестрового изображены на рисунке 4.

Скачать файл