














Тема 1. Теоремы о дифференцируемых функциях
1. Теоремы Ферма, Ролля, Лангража, Коши.
2. Правоило Лапиталя.
Теорема Ферма. Если функция у = f(x) дифференцируема в точке х0 и имеет в этой точке экстремум, то ее производная при х = х0 обращается в нуль, т. е. f´(x0) = 0.
Теорема Ролля. Если функция f(x) непрерывна на [a, b] и дифференцируема в интервале (a, b), а на концах отрезка имеет равные значения f(a) = f(b), то в интервале (a, b),найдется хотябы одна точка с, в которой производная равна нулю.
Теорема Лагранжа. Если функция f(x) непрерывна на [a, b] и дифференцируема в интервале (a, b), то в интервале (a, b) найдется хотя бы одна точка с, в которой:
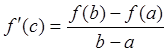 .
.
Теорема
Коши. Если у = f(x) и у = φ(х) – две
функции, непрерывные на [a, b] и дифференцируемые на (a, b), причем ![]() для всех
для всех ![]() , то между a и b найдется
точка с, такая что
, то между a и b найдется
точка с, такая что 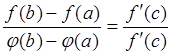 .
.
Правило Лопиталя. Если функции f(x) и q(х) дифференцируемы в некоторой окрестности точки
х0 за исключением, быть может, самой точки х0,
причем в этой окрестности ![]() , и если
, и если ![]() , или
, или ![]() , то
, то 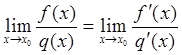 .
.
Тема 2. Производные и дифференциалы высших порядков
1. Определение дифференциала.
Пусть функция ![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки ![]() . Тогда если существует
такое число А, что приращение
. Тогда если существует
такое число А, что приращение ![]() этой функции в точке
этой функции в точке ![]() , соответствующее приращение
, соответствующее приращение ![]() аргумента, представимо в виде:
аргумента, представимо в виде:
![]() , где
, где ![]() то
функция f(x) называется дифференцируемой в точке
то
функция f(x) называется дифференцируемой в точке![]() . При этом главная, линейная относительно
. При этом главная, линейная относительно ![]() , часть этого приращения, т.е.
, часть этого приращения, т.е. ![]() называется дифференциалом функции в
точке
называется дифференциалом функции в
точке ![]() и обозначается
и обозначается ![]() или
или ![]() .
.
Пусть имеется функция у = f(x). Производную ![]() этой
функции будем называть первой производной. Второй производной (производной
второго порядка) функции у = f(x) называется производная от ее первой
производной. Обозначается:
этой
функции будем называть первой производной. Второй производной (производной
второго порядка) функции у = f(x) называется производная от ее первой
производной. Обозначается:
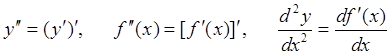 .
.
Аналогично определяется третья, четвертая и т. д. производная. п-ой производной функции у = f(x) называется производная ее (п – 1)-ой производной. Обозначается:
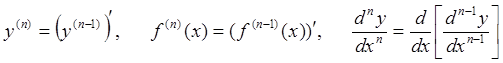 .
.
Если х – независимая переменная и у = f(x) –
дифференцируемая функция, то ![]() . Этот дифференциал
будем называть дифференциалом первого порядка. Считая dх постоянной,
заключаем, что df(x) – функция одной переменной х.
Предположим, что функция f(x) имеет п последовательных
производных:
. Этот дифференциал
будем называть дифференциалом первого порядка. Считая dх постоянной,
заключаем, что df(x) – функция одной переменной х.
Предположим, что функция f(x) имеет п последовательных
производных:
![]() .
.
Дифференциалом второго порядка функции у = f(x) называется
дифференциалом от дифференциала первого порядка этой функции т. е. d2y = d[dy], или ![]() .
.
Тема 3. Исследование функций с помощью производной
5. схема исследования функции.
Теорема (достаточный признак возрастания). Пусть функция у = f(x) непрерывна и дифференцируема на отрезке
[а, b]. Если для всех ![]()
![]() ,
то функция возрастает на [а, b].
,
то функция возрастает на [а, b].
Теорема (достаточный признак убывания). Пусть функция у = f(x) непрерывна и дифференцируема на [а, b],
если для всех ![]()
![]() , то
функция убывает на [а, b].
, то
функция убывает на [а, b].
Точки максимума и минимума функции у = f(x) называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Понятие экстремума носит локальный характер. Это наибольшее и наименьшее значение функции по сравнению с близлежащими значениями.
Теорема. Пусть функция у = f(x) дифференцируема в некоторой окрестности точки х0. Если в точке х0 производная функции равна нулю и меняет знак при переходе через эту точку, то х0 является точкой экстремума, причем:
1. х0 – точка максимума, если знак меняется с “+” на “–“.
2. х0 – точка минимума, если знак меняется с “–“ на “+”.
Теорема. Если в точке х0 первая производная функции у = f(x) равна нулю, а вторая производная отлична от нуля, то х0 является точкой экстремума, причем:
1. х0
– точка минимума, если ![]() .
.
2. х0
– точка максимума, если ![]() .
.
График функции у = f(x) называется выпуклым вниз на данном отрезке, если он целиком расположен выше касательной в его произвольной точке.
График функции у = f(x) называется выпуклым вверх на данном отрезке, если он целиком расположен ниже касательной в его произвольной точке.
Теорема. Если вторая производная функци у = f(x) в данном промежутке положительна, то
график функции является выпуклым вниз в этом промежутке. Если ![]() в данном промежутке, то график функциии
является выпуклым вверх в этом промежутке.
в данном промежутке, то график функциии
является выпуклым вверх в этом промежутке.
Теорема. Если в точке х0 вторая производная функции у = f(x) обращается в нуль
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.