Вероятность Р называется надежностью, или доверительной вероятностью оценки значения 6 с помощью выборочной функции 0*. Обычно надежность задается заранее, исходя из практических сообра-жений, и, как правило, принимается близкой к единице: 0,95; 0,99 или 0,999.
Пусть вероятность Р осуществления неравенства |0 — 6* |<б равна р:
Как отмечает А С. Чеботарев, теоретически можно доказать, что в подавляющем большинстве распределение случайных результатов измерений подчиняется нормальному закону распределения вероятностей. Согласно свойствам нормального распределения, выборочное среднее х является наивероятнейшим значением генеральной средней, которая в рассматриваемом случае представляет собой значение измеряемой величины. В качестве меры точности метода измерения в «теории ошибок измерений» принято среднее квадратическое отклонение ряда результатов измеренийгде хг — отдельный результат измерения, х — выборочное среднее (среднее из результатов измерений), п—число результатов измерений.
Величина ст в «теории ошибок измерений» называется средней квадратической погрешностью (погрешностью отдельного измерения).
В нефтяной геологической литературе среднюю квадрати ческую погрешность измерения принято обозначать буквой m в отличие от среднего квадратического отклонения совокупности значений признака, которое обозначается буквой 0.
Во многих случаях нас интересует точность не отдельного определения пористости, мощности или какого-либо другого геолого-физического свойства нефтегазоносного пласта, а вычисляемого по данным измерений среднего значения. На использовании средних основан, например, вариант среднего арифметического объемного метода подсчета запасов.
В математической статистике доказывается, что рассеяние среднего значения меньше, чем рассеяние единичных результатов измерений, и, следовательно, меньшей будет погрешность определения среднего значения. Она связана с погрешностью единичного измерения следующим соотношением:
![]()
где т- — погрешность определения среднего значения; т — погрешность отдельного измерения; п — число результатов измерений (объем выборки), по которым вычислялось среднее значение; t— гарантийный коэффициент, обеспечивающий получение величины т- с требуемой надежностью (т. е. доверительной вероятностью).
Погрешность т- возникает вследствие влияния погрешностей измерения отдельных значений величины х, по результатам которых определяется х. Но величина х находится неточно не только в связи с наличием погрешностей измерений, но и потому, что при вычислении х используются не все возможные значения х, а лишь некоторые, измеренные в точках наблюдения. Возникающая при этом погрешность в называется погрешностью репрезентативности (т. е. погрешностью, обусловленной степенью представительности результатов измерений). Она вычисляется по формуле, аналогичной (III.5):
где ох — среднее квадратическое отклонение результатов измерения х в точках наблюдения от х; п — число точек наблюдений; t— гарантийный коэффициент.
Подробное рассмотрение вопросов оценки точности различных измерений и осуществляемых на их основе определений и построений в нефтяной геологии можно найти в книге [«Оптимизация », 1976]. Использование результатов оценки точности при организации разведочных работ показано в § 5 настоящей главы.
Способы построения доверительных интервалов для статистических оценок числовых характеристик генеральных совокупностей рассматриваются в любом пособии по математической статистике, в частности, в работе [Дементьев Л. Ф., Жданов М. А., Кирсанов А. Н., 1977].
Рис. 3. Соотношение формальных точек при разных методах опробования пласта в одной скважине.
/ — скважина; 2 — образец породы, поднимаемый из скважины; 3 — породы-неколлекторы; 4 — породы-коллекторы; границы области воздействия: / — геофизических и гидродинамических (при стационарных режимах) методов исследования, L— гидродинамических методов при нестационарных режимах
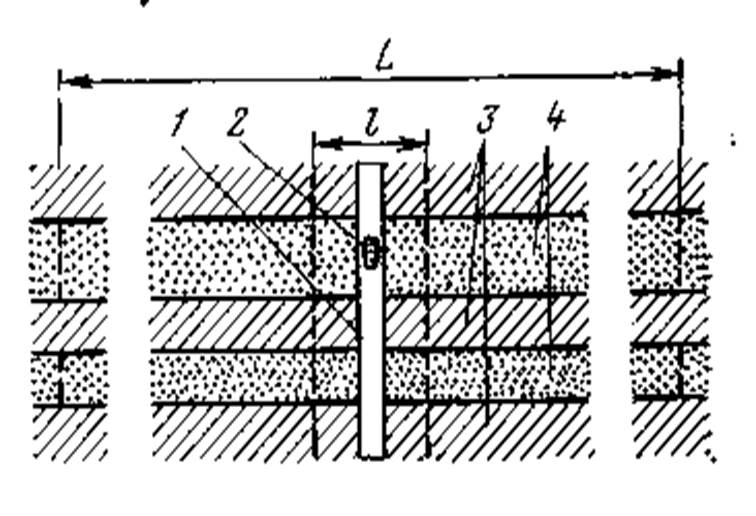
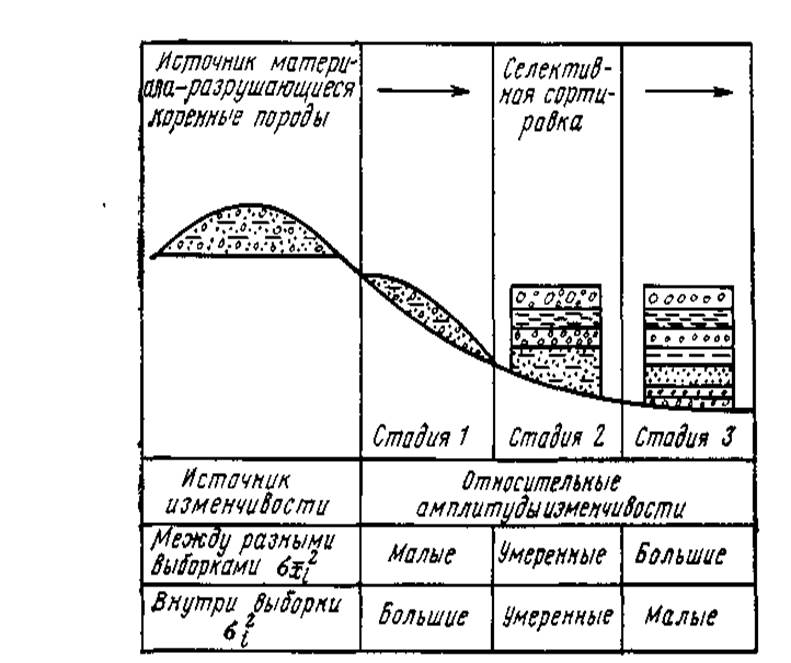
Рис. 5. Схема процесса седиментации и принципы опробования осадочных пород (по Дж. Гриффитсу, 1971 г.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.