Расчет линейной следящей системы для дистанционного управления углом положения суппорта

Функциональная схема.

 

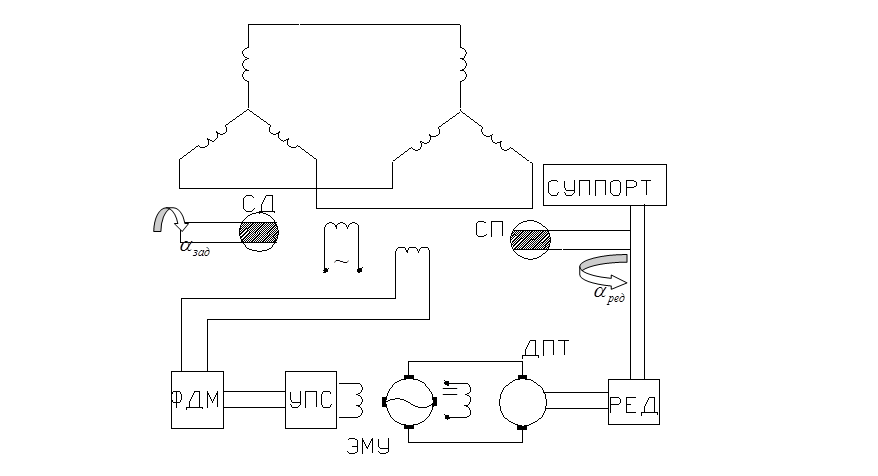
Задающий вал связан с выходным валом по угловому положению сельсинной парой, реализующей обратную связь. Выходное напряжение СП по переменному току преобразуется с помощью ФДМ (фазноволновой Д-модулятор), усиливается по напряжению с помощью УПТ (усилитель постоянного тока), поступает на управляющую обмотку ЭМУ (электромагнитный усилитель). Нагрузкой ЭМУ является якорная обмотка ДПТ (двигатель постоянного тока) с независимым возбуждением. Двигатель через редуктор связан с суппортом, являющимся нагрузкой следящей системы СС.

Задание к расчёту:

1.  Составить передаточные функции функциональных элементов, найти  ПФ разомкнутой и замкнутой АС и ПФ для ошибки. Построить ЛЧХ разомкнутой АС.

2.  Определить устойчивость исходной системы по Гурвичу и Михайлову. По ЛЧХ оценить устойчивость исходной системы по Найквисту.

3.  Спроектировать последовательное корректирующее устройство, обеспечивающее следующие качественные точностные показатели:

     а) перелегулирование            ;

     б) время переходного процесса               

     в) установившуюся ошибку по скорости         при заданной скорости вращения                                    заданного вала равной 10 [град/сек].

4.  Построить переходный процесс скорректированной схемы :

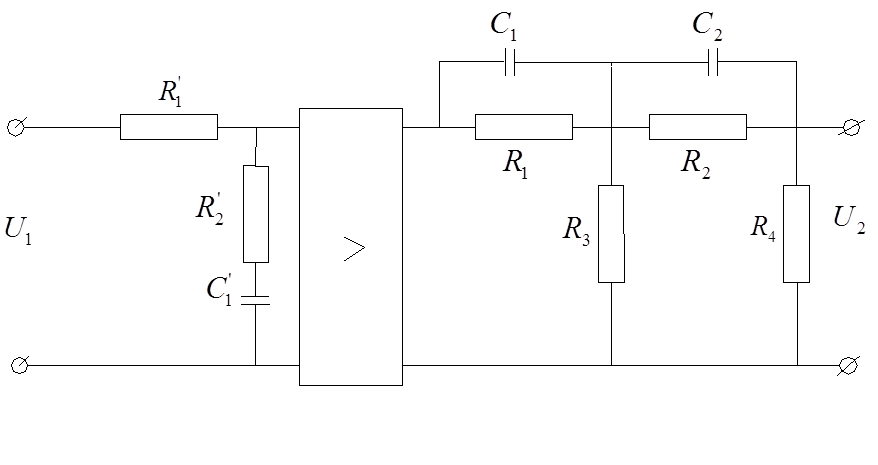
Структурная схема.

                                                                                                                              

 

Дифференциальные уравнения, описывающие элементы рассматриваемой САР:

1)  Сельсивная пара с ФДМ:

 

2)  Усилитель постоянного тока УПТ:

3)  ЭМУ (электронный усилитель):

 

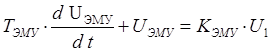4) 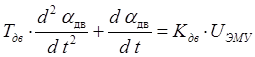 ДПТ с независимым возбуждением :

5)  Редуктор:

                

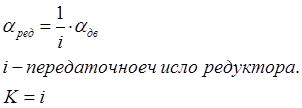
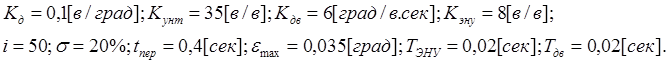Дано:

Решение:

I Запишем ПФ функциональных элементов:

  1) ПФ сельсинной пары  с ФДМ, для которой входным воздействием является

                        , а выходным величина        . Сельсинная пара с ФДМ-идеальное усиленное звено.                          :

 

 2) ПФ усилителя постоянного тока, для которой входным воздействием является        , а входным величина        . УПТ-идеальное усилительное звено.

 

  3) ПФ электромагнитного усилителя, для которой входным воздействием является

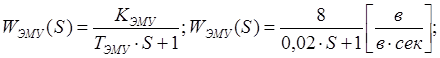        , а выходным величина       . ЭМУ-оперативное звено 1-го порядка.

4) ПФ двигателя постоянного тока, для которой входным воздействием является         ,

а выходным величина      . ДПТ-инерциальное интегрирующее звено.

 

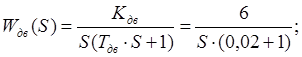 6) ПФ редуктора, у которой входным воздействием является      , а выходным       .

Редуктор-идеально усиленное звено.

ПФ разомкнутой АС:

Оборвав ООС, получим разомкнутую АС из 5-ти последовательно соединенных функционально элементов. При этом выходная величина каждого предыдущего

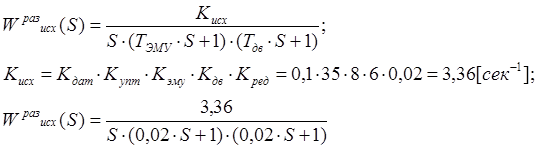является входным воздействием каждого последующего элемента.

ПФ замкнутой АС:

Поскольку данная замкнутая АС имеет единичную ООС, то передаточная функция для неё будет иметь вид:

 

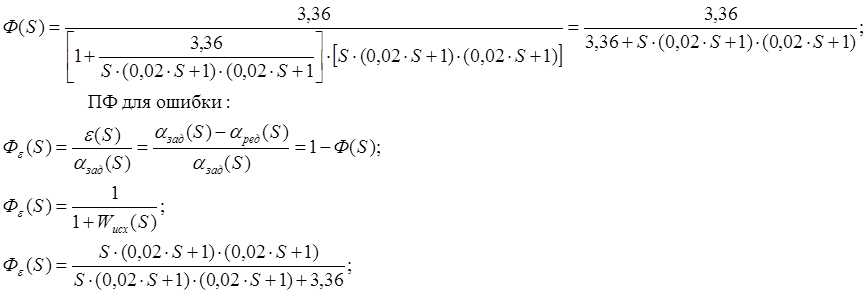Построение ЛАЧХ и ЛФЧХ разомкнутой АС:

Асимптотическая логарифмическая амплитудно-частотная характеристика состоит из трёх асимптот:

1. От 0 до        , под наклоном-20дб/дк, т.к.

        первый порядок астатизма.

   От        до         , под наклоном-40дб/дк, т.к.

        второй порядок астатизма.

   

  От       и далее, под наклоном-60дб/дк, т.к.

        третий порядок астатизма.

В данном случае асимптота под наклоном – 40 дб/дк не строиться, т.к. частоты сопряжений равны.

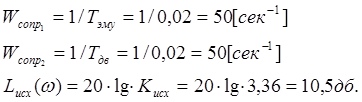Частоты сопряжения для ЛАЧХ:

Построение ЛФЧХ отдельно для каждого из трёх различных звеньев:

 

1	-1,15	-1,15	-2,30
10	-11,3	-11,3	-22,6
100	-63,4	-63,4	-126,8

Сопоставление ЛАЧХ и ЛФЧХ позволит сделать вывод, что исходная система устойчива.

Необходимо построить такую желаемую характеристику, которая обеспечила требуемые

               .

Построение  Lж(w) начинается с низкочастотной области. Её уровень определяется величиной коэффициента передачи Kж:

Поскольку рассматриваемая система является астатической 1-го порядка, то:

 

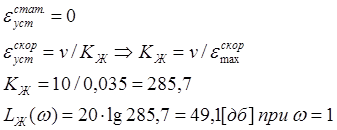Наклон асимптоты среднечастотной области желательно выбрать – 20 дб/дк, т.к. соответствует увеличению демпфирующих свойств системы.

Исходя из заданных требований:

 

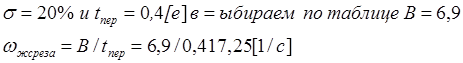Асимптоту высокочастотной области строим с максимально отрицательным наклоном, т.е. – 60дб/дк,что определяет подавление высокочастотных полях.

Длина СЧ асимптоты ограничена двумя частотами ординаты которых равны 15-20 дб. Сопряжение СЧ и НЧ асимптоты возможно с помощью асимптоты с наклоном – 40 дб/дк.

II Анализ устойчивости исходной АС:

1.  По Гурвину.

Сопоставим  характеристический многочлен                

 

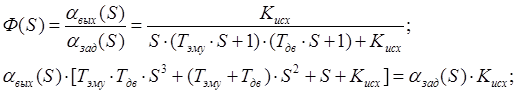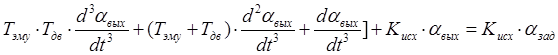Применив к этому выражению обратное преобразование Лапласа, получим дифференциальное уравнение, описывающее рассматриваемую АС.

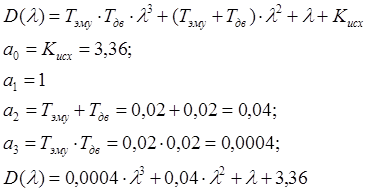Для этого диф. Ур. Можно составить характеристический многочлен:

 

Для того, чтобы           соответствовал устойчивости АС необходимо и достаточно, чтобы были положительны все глав. Диагональные миноры определителя Гурвина:

 

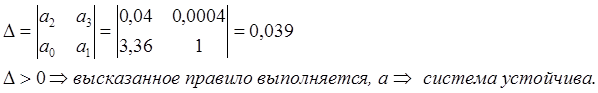   1.По Михайлову.

АС будет устойчива, если при возрастании частоты от 0 до ¥, вектор D(jw) повернётся на угол pn/2, где n – степень урав. D(l)=0 или, что тоже самое, если характер – кая кривая

При изменении частоты от 0 до ¥,начиная с положительной действительной оси, обходит последовательно в положительном направлении( против часовой стрелки), n – квадратов.

 

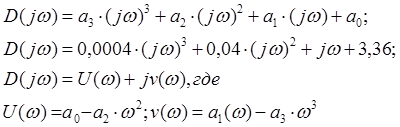Для построения хар-кой кривой достаточно определить точки пересечения с действительной осью:

 

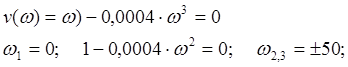Все отрицательные корни не удовлетворяют возрастанию частоты от 0 до ¥. След-но пересичение с осью произойдёт при w1=0 и w2=50

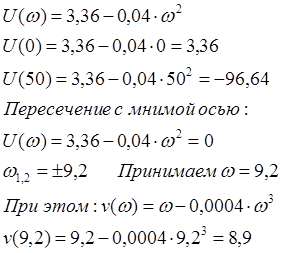При этом:

 

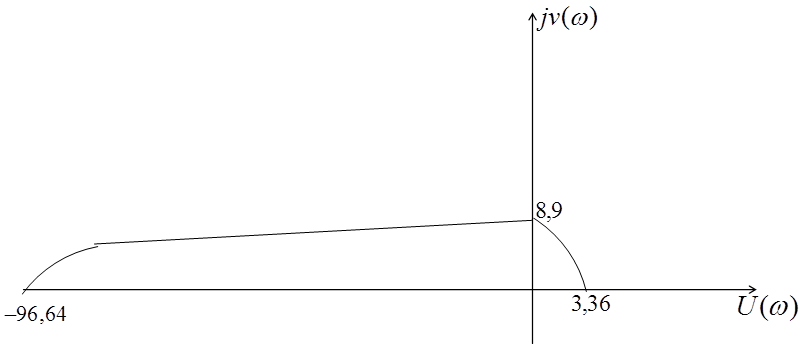По виду кривой можно сделать вывод, что рассматриваемая АС устойчива.

2.  По Найквисту:

Рассмотрев логарифмические хар-ки разомкнутой системы видно, что при всех частотах, при которых ЛАЧХ положительна, значение фазы не превышают -p (-180°), т.е. wсреза <wp. Следовательно система устойчива в замкнутом состоянии.

III Для построения последовательно корректирующего устройства необходимо определить его ЛАЧХ, а для этого необходимо найти разомкнутую м/д желаемой ЛАЧХ и ЛАЧХ исходной разомкнутой АС.

Вычисление производится графически по ф-ле:

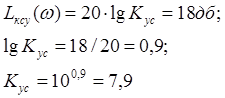Коэф. Усиления этого усилителя определяется графически:

Схема корректирующего устройства