На рис.3 показана розрахункова схема пневмоприводу, головним елементом якої є поршневий пневмоциліндр односторонньої дії. Поршень пневмоциліндру є показаним в момент руху вгору. Його положення знаходиться поточною координатою x, яка відраховується від умовного нуля. В вихідному положенні поршня (показано пунктиром) x=0, але між поршнем і кришкою циліндру завжди є деякий невеличкий об'єм, який називається шкідливим об’ємом циліндру. Фіктивна координата x0, що показана на розрахунковій схемі, характеризує мінімальний розрахунковий об’єм робочої порожнини циліндру, який повинен бути наповнений стиснутим до деякого тиску повітрям, перш ніж поршень почне рухатися. Фактичний мінімальний об’єм робочої порожнини дорівнює додатку шкідливого об’єму до об’єму трубопроводу, що зв’язує робочу порожнину з виходом пневморозподілювача. Однак при розрахунку треба враховувати, що умови
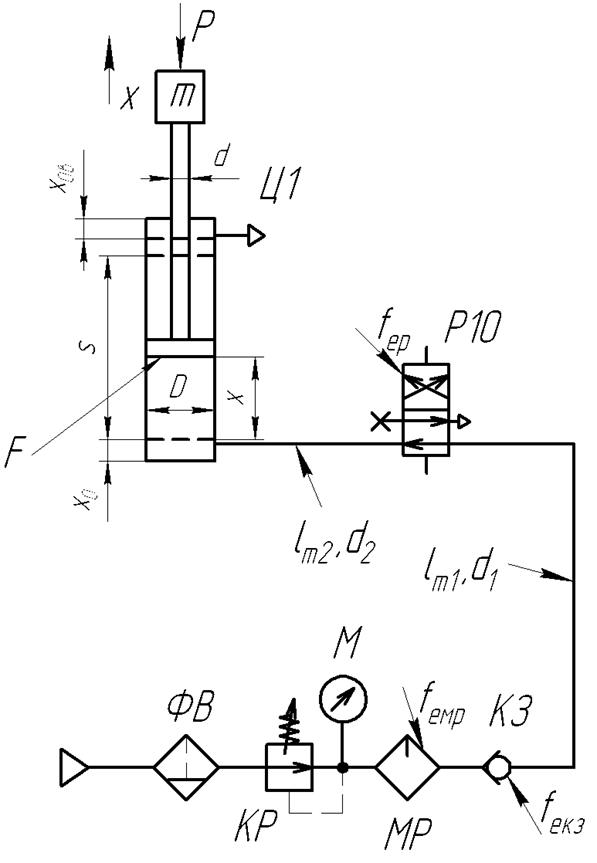 |
Рис. 2
є однаковими, тому фактичний об’єм трубопроводу замінюється його розрахунковим (приведеним) значенням. Координата x0 розраховується за формулою:
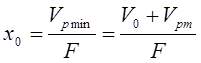 , де
Vp min – мінімальний розрахунковий об’єм робочої порожнини; F –
площа поршня з боку робочої порожнини; V0 – шкідливий об’єм
циліндру; Vрт – розрахунковий (приведений) об’єм трубопроводу.
, де
Vp min – мінімальний розрахунковий об’єм робочої порожнини; F –
площа поршня з боку робочої порожнини; V0 – шкідливий об’єм
циліндру; Vрт – розрахунковий (приведений) об’єм трубопроводу.
![]()
де s – робочий хід привода.
Пізніше знайдемо, що Vpmн = 1,384·10-3 м3.
Підставимо значення в (3) і знайдемо х0:
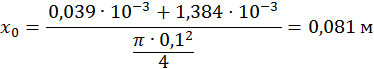
Так само знаходиться координата xов , що характеризує мінімальний розрахунковий об’єм порожнини вихлопу:
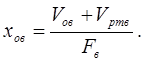
де Fв – площа поршня з боку порожнини вихлопу;
Vов – шкідливий об’єм вихлопу циліндра;
![]() – розрахунковий об’єм лінії вихлопу.
– розрахунковий об’єм лінії вихлопу.
![]()
де s – робочий хід привода.
Пізніше знайдемо, що Vpmв = 0,39·10-3 м3.
Підставимо значення в (4) і знайдемо xов:
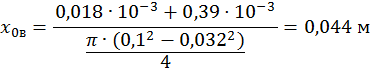
5.3. Знаходження пропускної здатності пневмоліній
5.3.1. Знаходження пропускної здатності напірної пневмолінії
Так як пневмолінія нашої схеми складається з двох частин трубопроводу, що зв’язують між собою елементи пневмоапаратури, на яких будемо визначати пропускну здатність напірної пневмолінії, то ефективна площа перетину являє собою приведену величину.
При послідовному з’єднанні елементів та участків напірної пневмолінії маємо:
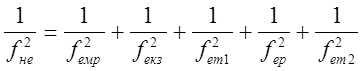
Знайдемо ефективну площу розподільника, маслорозпилювача та зворотного пневмоклапану за формулою:
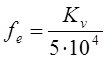 (12)
(12)
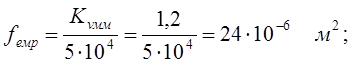
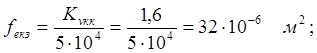
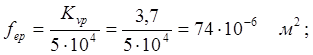
Знайдемо
![]() ,
, ![]() , для цього знайдемо коефіцієнт сумарних
витрат
, для цього знайдемо коефіцієнт сумарних
витрат ![]() ,
, ![]() за
формулою:
за
формулою:
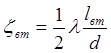
де
l = 0,025 –
коефіцієнт тертя для повітря, d – діаметр трубопроводу; ![]() - довжина ділянки трубопроводу.
- довжина ділянки трубопроводу.
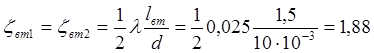
За
величиною ![]() ,
, ![]() ,
використовуючи графік m=j(z)(рис.4),
знаходимо величину m1,
m2,
m1 =
m2
= 0,6
,
використовуючи графік m=j(z)(рис.4),
знаходимо величину m1,
m2,
m1 =
m2
= 0,6
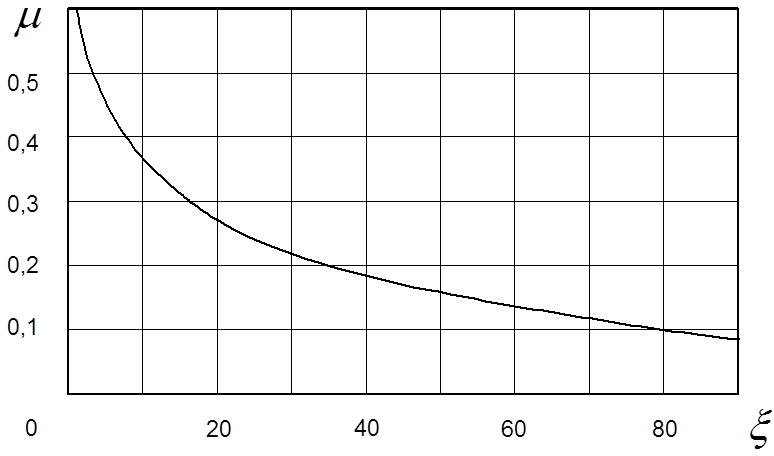
Рис. 3
Рахуємо ефективну площу:
![]()
де fт – площа перетину трубопроводу.
![]()
![]()
Підставивши отримані значення, отримаємо:
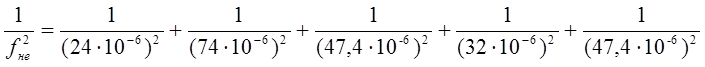
![]()
5.3.2. Знаходження пропускної здатності зливної пневмолінії
Так як пневмолінія нашої схеми складається з трубопроводу, що зв’язують між собою елементи пневмоапаратури, на яких будемо визначати пропускну здатність зливної пневмолінії, то ефективна площа перетину являє собою приведену величину.
При послідовному з’єднанні елементів та участків зливної пневмолінії маємо:
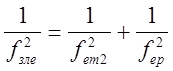 (11)
(11)
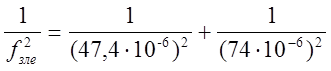
![]()
5.4. Врахування об’ємів трубопроводів при динамічному розрахунку
5.4.1. Врахування об’ємів трубопроводів при динамічному розрахунку напірної пневмолінії
Розрахунковий (приведений) об’єм лінії нагнітання визначається з виразу:
Vртн = Kv1·Vтн1+Kv2·Vтн2,
де Vтн – фактичний об’єм напірного трубопроводу;
Kv - коефіцієнт приведення розподіленого об’єму до зосередженого.
Коефіцієнт Kv знаходиться за формулою
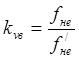 , де
, де
![]() – ефективна площина перетину лінії нагнітання;
– ефективна площина перетину лінії нагнітання;
![]() – ефективна площина перетину тієї ж
пневмолінії, але знайдена з урахуванням половини гідравлічного опору ділянки
трубопроводу, для якого визначається розрахунковий об’єм.
– ефективна площина перетину тієї ж
пневмолінії, але знайдена з урахуванням половини гідравлічного опору ділянки
трубопроводу, для якого визначається розрахунковий об’єм.
Знайдемо
ефективну площу на ділянках ![]() ,
, ![]() , із якої визначимо розрахунковий об’єм:
, із якої визначимо розрахунковий об’єм:
![]() .
.
Знайдемо
для половини ділянки значення ![]() :
:
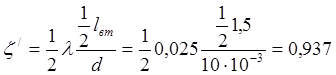
За
величиною ![]() , використовуючи графік m=j(z)(рис.4),знаходимо
величину m', m' =0,7.
, використовуючи графік m=j(z)(рис.4),знаходимо
величину m', m' =0,7.
Підставимо знайдені значення та отримаємо:
![]()
Щоб
знайти ![]() використаємо вираз (22):
використаємо вираз (22):
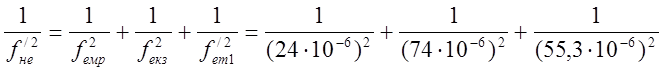
![]()
Знайдені значення підставимо:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.