Методичні вказівки до виконання лабораторних робіт з курсу «Деталі машин», страница 10

4. Основні характеристики досліджуваного підшипника;

5. Результати випробувань і розрахунків (навести в табл. 5.1);

6. Графіки залежності коефіцієнта тертя f від радіального навантаження на підшипник F_r і частоти обертання вала n;

7. Аналіз одержаних результатів. Висновки.

Таблиця 5.1

Результати вимірів і розрахунків

Частота обертання підшипника, хв-1	Навантаження Fr на підшипник		Зрівноважувальна сила F		Коефіцієнт тертя f
	Поділки індикатора	Н	Поділки індикатора	Н
600	100
	200
	300
	400
	500
1400	100
	200
	300
	400
	500

Графік залежності f від F_r та n

Висновки з роботи

«_____»_______________200___р.                                                                   Підпис студента(__________)

Підпис викладача(__________)

ЛАБОРАТОРНА РОБОТА №6

Визначення критичної частоти обертання вала

Мета роботи-визначити теоретично і експериментально критичну частоту оберту вала та виявити вплив на неї маси та положення закріплених деталей.

Теоретичні відомості

Такі деталі, як зубчасті колеса, шківи, муфти та інші деталі встановлюють на валах. Неточність виготовлення вала та закріплених на ньому деталей, а також деформації від навантажень, приводять до зміщення е центра їх ваги відносно їх геометричної осі обертання і виникнення відцентрових сил, які викликають поперечні коливання. Коли частота власних коливань вала збігається з частотою зміни зовнішніх сил, настає резонанс, а відповідну йому частоту обертання вала n_кр.т, хв^-1, називають критичною і теоретично визначають за формулою

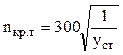,                                                                        (6.1)

де у_ст-статичний прогин вала, см. Статичний прогин вала у_ст (силою ваги нехтують) можна визначити за формулою

, де F-вага деталі, що обертається, Н; С-жорсткість вала у місці розташування деталі, що обертається, Н/см. Жорсткість вала визначають за формулою

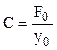, де F₀-додаткове навантаження у місці розташування деталі, що обертається (навантаження здійснюється в статичному стані вала), Н; у₀-прогин вала під дією ваги вантажу, см. Типові криві залежності динамічного прогину у_Д вала від швидкості його обертання зображено на рис. 6.1. На рисунку показано що, якщо в експерименті при однаковому фіксованому прогині у визначити частоту обертання n₁ вала на вході та виході з резонансу n₂, то критичну частоту обертання вала можна знайти як

,                                                                      (6.2)

що і реалізується в цієї роботі.

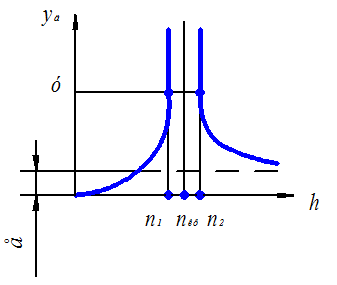
Рис. 6.1 Крива залежності динамічного прогину у_Д вала від швидкості його обертання

При обертанні вала його динамічний прогин у докритичній області визначають за формулою

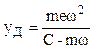, де m-маса коливної системи; w-кутова швидкість обертання вала. У міру збільшення кутової швидкості вала збільшується його прогин, і, коли знаменник , зростає до нескінченності, що призводить вал до поломки. Швидкість, коли  є критичною. Динамічний прогин вала в закритичній області визначають за формулою

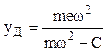
У цьому випадку з подальшим збільшенням кутової швидкості стріла прогину швидко зменшується, , , тобто наступає явище самоцентрування вала. Щоб уникнути руйнування валів, які працюють у закритичній області, необхідно швидко переходити через критичну швидкість. Вали, що працюють у докритичній області, називають жорсткими, а в закритичній-гнучкими. Розрахунок валів для запобігання поперечних коливаням полягає у перевірці умови відсутності резонансу під час усталеного режиму роботи. Відповідно до цієї умови фактична частота обертання валів неповинна знаходитись у межах від 0,7 n_кр до 1,3 n_кр тобто