Проблема – нерешенная или наиболее существенная задача. Выделение некоторой области знаний или комплекса проблем.
Задача – требование определить результат в соответствии с поставленной целью при выбранных данных, граничных условиях и ограничениях.
Модель – это такой материальный или мыслимый объект, который в процессе познания (исследования) замещает объект-оригинал, сохраняя некоторые важные для данного исследования его черты и свойства.
Моделирование – процесс построения модели объекта-оригинала.
Множество – объединение в единое целое определенных элементов.
Пространство – множество, наделенное нормой или метрикой.
IV. Практика использования научных знаний
1. Целевой анализ исследований
1.1. Научные знания используются при обучении и в научных исследованиях. Для практического использования научных знаний всегда требуется определить систему целей и сформулировать задачи целедостижения (рис. 5). Такая ситуация возникает при написании аттестационных работ.
1.2 Система целей – это совокупность концептуально определенных целей. В соответствии с определением "система" исследователем для одного и того же объекта, явления может быть построено несколько систем целей, состоящих из таких целей как, например:
· глобальная цель (предназначенность системы);
· главная цель – исследование функций и/или структуры системы;
· стратегические и тактические цели создания системы;
· производственные, экономические, социальные цели и т.п.
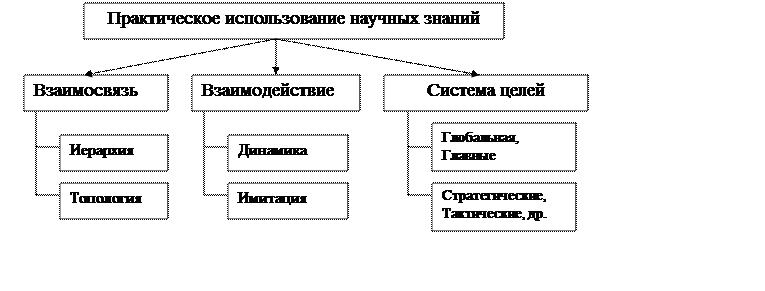
Рис. 6. Основные проблемы использования научных исследований
V. Математические методы решения научных задач
1. Разработкой математических методов решения научных задач занимается математика. Математика – это наука о количественных отношениях и пространственных формах действительного мира. Различают фундаментальную и прикладную математику. По другой классификации в математике различают основы (начала), разделы (совокупность разделов) и теории.
2. Решение любой научной задачи обязательно предусматривает разработку или использование различных математических методов. С учетом стадий решения научных задач выделяют:
- методы содержательной постановки задач;
- методы математической постановки задач;
- методы численного решения задач (численные методы);
- методы алгоритмизации научных задач;
- методы программирования задач;
-методы ускоренного получения практических результатов (натурный и(или) вычислительный эксперимент);
- методы сравнения практических и теоретических результатов.
3. Существуют основы (начала) дискретной и непрерывной математики. В началах математики выделяются разделы четкой или детерминированной, стохастической или вероятностной, нечеткой или размытой, математики.
4. Математические теории решения научной задачи.
4.1. Разработкой методов содержательной постановки научных задач занимаются: теория оптимизации, теория управления, теория адаптации, теории принятия решения, теория массового обслуживания, теория расписаний, теория машин и механизмов, теория графов, теория игр, теория вероятностей, теория волновых процессов и т.д. Особо следует выделить ТОЭ, ТАУ, теоретическую физику, теплотехнику, радиотехнику, информатику, кибернетику и многие другие прикладные теории технических систем.
4.2. Разработкой методов математической постановки задач занимаются теория моделирования и теория принятия решений.
4.3. Разработкой методов решения задач занимается теория алгоритмов и теория численных методов.
4.4. В соответствии с обилием исследуемых свойств объектов любая научная задача ее исследования, как правило, декомпозируется на корневую и вспомогательные. С точки зрения методологии решения корневые, как и вспомогательные задачи требуют для решения одних и тех же методов. При этом композиция – декомпозиция научной задачи находятся в диалектическом единстве. Процесс композиции-декомпозиции научной задачи всегда выполняется исследователем самостоятельно и требует апробации (обсуждения научной общественностью).
4.5. Корректность решения научной задачи может быть проверена исключительно путем численного решения, с последующей проверкой результатов на практике, т.е. путем проведения анализа сходимости практических и теоретических результатов.
VI. Основы теории моделирования
1. Основные понятия и определения:
Модель – упрощенный аналог явлений, процессов, предметов и объектов, сохраняющий их существенные свойства, служащие предметом их изучения.
Моделирование – исследование каких-либо явлений, процессов, предметов или объектов путем построения их модели. На идее моделирования базируется любой метод научного исследования, как теоретический, при котором используются формализмы, концепты или абстрактные модели, так и опытно экспериментальный, при котором используются материальные модели.
Формализация – это процесс построения субъектом исследования абстрактной формы представления (формальной модели) объекта исследования. Здесь найденная модель выступает как результат научного исследования в задачах управления, системного анализа и т.д.
Физическое моделирование – это построение субъектом исследования гносеологического образа объекта исследования с целью решения каких-либо научных задач в терминах физики. По аналогии определяются химическое, биологическое, психологическое, геологическое и т.п. моделирование.
Математическое моделирование – это построение субъектом исследования гносеологического образа объекта исследования с целью решения каких-либо научных задач в терминах математики. Математическое моделирование осуществляется с помощью интерпретации абстрактного образа объекта исследования в конкретную область его свойств.
Интерпретация в математическом моделировании - есть информационный процесс преобразования абстрактного математического объекта (АМО) в конкретную математическую модель (ММ) конкретного объекта на основе отображения непустого множества данных и знаний, определяющего АМО, и, называемого областью интерпретации, в информационное пространство данных и знаний, определяемое объектом моделирования, и, называемое предметной областью значений свойств объекта исследования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.