Задание
1. Решить задачу линейного программирования графическим и симплекс-методом.
![]()
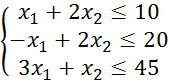
![]()
2. Найти оптимальный план закрепления потребителей за поставщиками однородного груза при условии минимизации затрат на перевозку, используя предоставленные ниже параметры
![]()
![]()
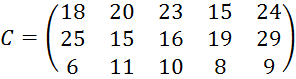
3. Решить игру с
заданными платежными матрицами а) 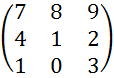 б)
б)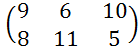
1. Решить задачу линейного программирования графическим и симплекс-методом.
![]()
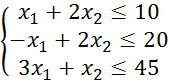
![]()
1) Графический способ
Строим опорную область.
![]()
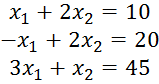
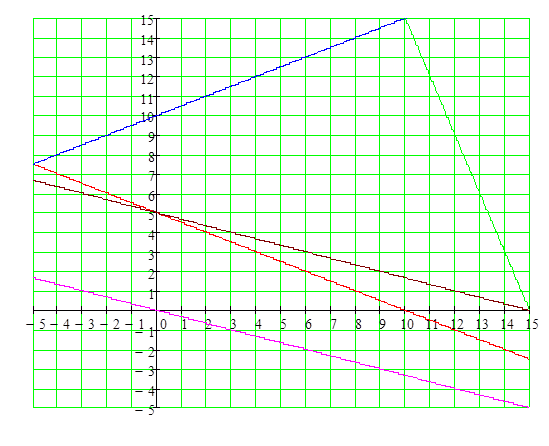
Рисунок 1 – Опорная область
Максимальному значению целевой функции соответствуют значения
![]() .
.
Значение целевой
функции при этом:
![]()
2) Симплекс-метод.
Приводим систему к
канонической форме, вводим выравнивающие коэффициенты ![]() :
:
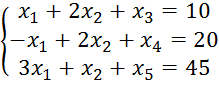
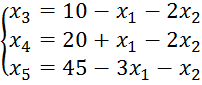
Базисному решению соответствуют нулевые значения
свободных переменных (![]() ).
).
![]()
Строим симплекс-таблицу.
Для выбора разрешающего столбца выбирается столбец свободной переменной с отрицательной оценкой.
Для выбора разрешающей
строки в разрешающем столбце находим отношение ![]() только для положительных
коэффициентов. Наименьшее значение дроби определяет разрешающую строку.
только для положительных
коэффициентов. Наименьшее значение дроби определяет разрешающую строку.
Таблица 1 – Симплекс-таблица
|
|
Базис |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
0 |
0 |
0 |
||||||
|
|
|
|
|
|
||||||
|
исх. сист. |
0 |
|
10 |
1 |
2 |
1 |
0 |
0 |
14 |
10 |
|
0 |
|
20 |
-1 |
2 |
0 |
1 |
0 |
22 |
||
|
0 |
|
45 |
3 |
1 |
0 |
0 |
1 |
50 |
15 |
|
|
|
||||||||||
|
перв. итерац. |
1 |
|
10 |
1 |
2 |
1 |
0 |
0 |
14 |
5 |
|
0 |
|
30 |
0 |
4 |
1 |
1 |
0 |
36 |
30/4 |
|
|
0 |
|
15 |
0 |
-5 |
-3 |
0 |
1 |
8 |
||
|
|
||||||||||
|
втор. итерац. |
3 |
|
5 |
0,5 |
1 |
0,5 |
0 |
0 |
7 |
|
|
0 |
|
10 |
-2 |
0 |
-1 |
1 |
0 |
8 |
||
|
0 |
|
40 |
2,5 |
0 |
-0,5 |
0 |
1 |
43 |
||
|
|
||||||||||
Так как![]() положительны, то
положительны, то ![]() является максимальным, при
является максимальным, при ![]() ,
, ![]()
2. Найти оптимальный план закрепления потребителей за поставщиками однородного груза при условии минимизации затрат на перевозку, используя предоставленные ниже параметры
![]()
![]()
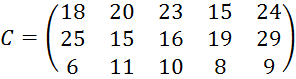
Методом минимального элемента составим опорный план перевозок.
Таблица 2 – Оптимальный план перевозок
|
150 |
140 |
115 |
225 |
220 |
||||||
|
300 |
75 |
18 |
20 |
23 |
225 |
15 |
24 |
|||
|
300 |
45 |
25 |
140 |
15 |
115 |
16 |
19 |
29 |
||
|
250 |
30 |
6 |
11 |
10 |
8 |
220 |
9 |
|||
Воспользуемся методом потенциалов.
Для расчета значений потенциалов составляем систему уравнений по нагруженным
клеткам ![]() , приняв
, приняв ![]() .
.
Таблица 3 – Метод потенциалов
|
150 |
140 |
115 |
225 |
220 |
|
|||||||
|
300 |
75 |
18 + |
20 |
23 |
225 |
15 – |
24 |
-7 |
||||
|
300 |
45 |
25 – |
140 |
15 |
115 |
16 |
● |
19 + |
29 |
0 |
||
|
250 |
30 |
6 |
11 |
10 |
8 |
220 |
9 |
-19 |
||||
|
|
25 |
15 |
16 |
22 |
28 |
|||||||
Для ненагруженных клеток рассчитываем значения их оценок по формуле
![]()
|
|
|
|
Значение целевой функции определим по формуле
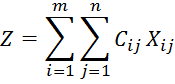
![]()
Для улучшения предыдущего плана составляем контур перераспределения нагрузки (см. таблицу 3). Исходный узел расположен в свободной клетке с положительным значением оценки. Догружаем клетки с «+» и разгружаем клетки с «–» на 45, получаем таблицу 4.
Таблица 4 – Метод потенциалов
|
150 |
140 |
115 |
225 |
220 |
|
|||||||
|
300 |
120 |
18 |
20 |
23 |
180 |
15 |
24 |
-4 |
||||
|
300 |
25 |
140 |
15 |
115 |
16 |
45 |
19 |
29 |
0 |
|||
|
250 |
30 |
6 |
11 |
10 |
8 |
220 |
9 |
-16 |
||||
|
|
25 |
15 |
16 |
19 |
25 |
|||||||
Для ненагруженных клеток рассчитываем значения их оценок:
|
|
|
|
Значения всех оценок свободных клеток отрицательны, поэтому данный план перевозок можно считать оптимальным.
Значение целевой
функции является минимальным
![]()
3. Решить игру с
заданными платежными матрицами а) 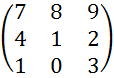 б)
б)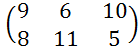
а) Максиминная стратегия I игрока:
![]()
![]()
![]()
![]()
Минимаксная стратегия II игрока:
![]()
![]()
![]()
![]()
Так как ![]() то точка
то точка ![]() является седловой и
является седловой и
![]() - чистая цена игры.
- чистая цена игры.
б) Графическим методом решим в смешанных стратегиях матричную игру со следующей платежной матрицей:
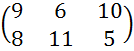
Определим выигрыш I
игрока,
если он выбирает свою первую стратегию с вероятностью ![]() , а вторую с вероятностью
, а вторую с вероятностью ![]() в случае, когда II
игрок выбрал свою первую стратегию.
в случае, когда II
игрок выбрал свою первую стратегию.
![]()
![]()
Определим выигрыш I
игрока,
если он выбирает свою первую стратегию с вероятностью ![]() , а вторую с вероятностью
, а вторую с вероятностью ![]() в случае, когда II
игрок выбрал свою вторую стратегию.
в случае, когда II
игрок выбрал свою вторую стратегию.
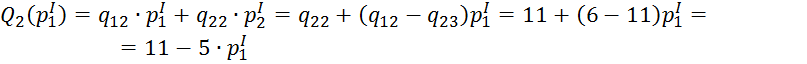
Определим выигрыш I
игрока,
если он выбирает свою первую стратегию с вероятностью ![]() , а вторую с вероятностью
, а вторую с вероятностью ![]() в случае, когда II
игрок выбрал свою третью стратегию.
в случае, когда II
игрок выбрал свою третью стратегию.
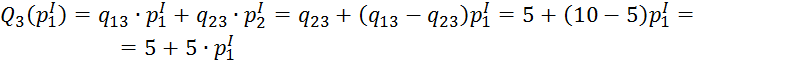
|
|
Рисунок 2 – Графическое решение матричной игры
Цена игры = 8.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.