























нагрузкой Р,
распределенной нагрузкой q, имеет две
кольцевых опоры: на внутреннем контуре (![]() ) и в
сечении
) и в
сечении ![]() . Геометрические размеры пластины, ее
толщину и механические характеристики материала пластины полагаем известными.
. Геометрические размеры пластины, ее
толщину и механические характеристики материала пластины полагаем известными.
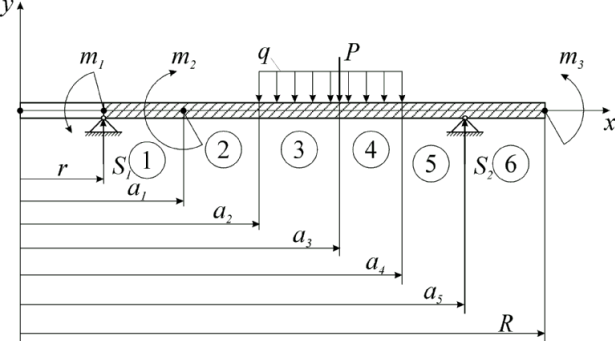
Рис.2.2. Расчетная схема кольцевой пластины (задача 2.2)
В
данном случае опорные реакции S1иS2не
могут быть определены из одного уравнения равновесия пластины ![]() .
.
Значения
начальных параметров ![]() и
и ![]() известны:
известны:
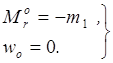 (2.8)
(2.8)
В данном случае пластина имеет шесть участков нагружения (показаны на рис.2.2). Общие уравнения изгиба пластины:
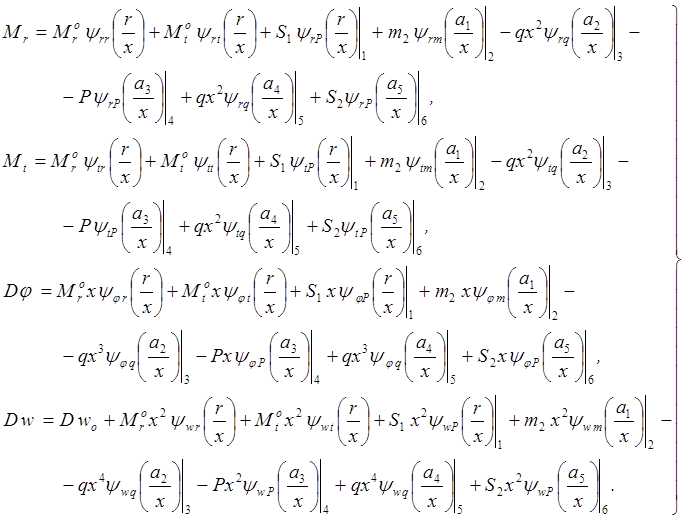 (2.9)
(2.9)
В уравнениях (2.9)неизвестны
начальный параметр ![]() и опорные реакции
и опорные реакции ![]() и
и ![]() .
Для их определения мы имеем в своем распоряжении:
.
Для их определения мы имеем в своем распоряжении:
- граничное условие на наружном контуре пластины:
![]() при
при ![]() ;
(2.10)
;
(2.10)
- уравнение равновесия пластины:
![]() ;
(2.11)
;
(2.11)
- условие,
накладываемое вертикальной связью на прогиб пластины при ![]() :
:
![]() .
(2.12)
.
(2.12)
Подставляем
условия (2.10) и (2.12) в уравнения (2.9) для радиального изгибающего момента ![]() и
и ![]() :
:
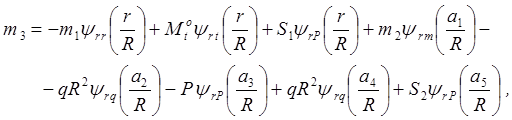 (2.13)
(2.13)
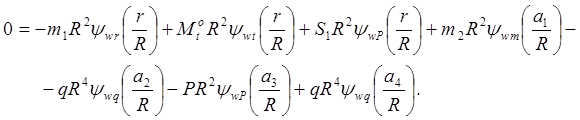 (2.14)
(2.14)
Решая совместно систему уравнений (2.11), (2.13) и (2.14), находим
неизвестные ![]() ,
, ![]() и
и ![]() . Затем,
задаваясь радом значений координаты x , по уравнениям (2.9) определяем изгибающие моменты
и перемещения в соответствующих сечениях пластины.
. Затем,
задаваясь радом значений координаты x , по уравнениям (2.9) определяем изгибающие моменты
и перемещения в соответствующих сечениях пластины.
2.2. Круглая пластина
Общие уравнения изгиба круглой пластины, записанные в форме метода начальных параметров, имеют вид:
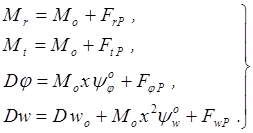 (2.15)
(2.15)
В уравнениях
(2.15) ![]() и
и ![]() -
начальные параметры (изгибающий момент и прогиб в центре пластины
-
начальные параметры (изгибающий момент и прогиб в центре пластины ![]() );
);
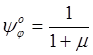 ,
, 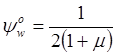 -
сопровождающие функции при начальных параметрах.
-
сопровождающие функции при начальных параметрах.
Грузовые
функции ![]() ,
, ![]() и
сопровождающие функции
и
сопровождающие функции ![]() ,
, ![]() являются
общими для круглых и кольцевых пластин. Для определения начальных параметров
используют граничные условия на наружном контуре пластины (см. табл. 2.1).
являются
общими для круглых и кольцевых пластин. Для определения начальных параметров
используют граничные условия на наружном контуре пластины (см. табл. 2.1).
3. Примеры численного расчета пластин
Задача 3.1
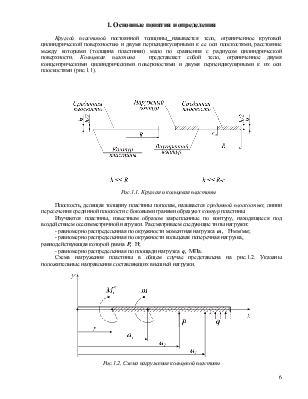
Выполнить расчет кольцевой пластины (рис. 3.1) по следующим данным:
r = 200 мм, h = 20 мм,
R =1000 мм, μ = 0.3,
a = 600 мм, E = ![]() МПа.
МПа.
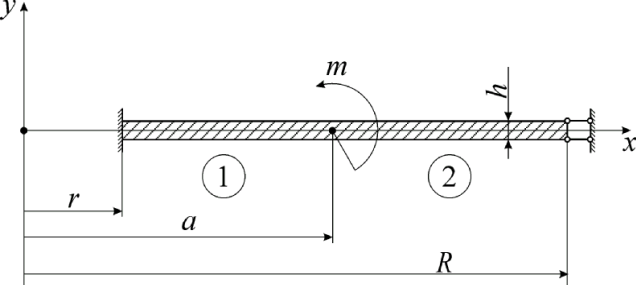
Рис.2.3. Расчетная схема кольцевой пластины (задача 3.1)
Предел
текучести материала пластины ![]() = 240 МПа. Коэффициент
запаса прочности по пределу текучести
= 240 МПа. Коэффициент
запаса прочности по пределу текучести ![]() = 1,5.
= 1,5.
Определить
радиальный и кольцевой изгибающие моменты, углы поворота и прогибы пластины, а
также допускаемую величину моментной нагрузки ![]() .
.
Из условия равновесия пластины ![]() следует,
что вертикальная реакция опоры на внутреннем контуре равна нулю. Пластина имеет
два участка нагружения (показаны на рис.3.1). Начальный параметр
следует,
что вертикальная реакция опоры на внутреннем контуре равна нулю. Пластина имеет
два участка нагружения (показаны на рис.3.1). Начальный параметр ![]() равен нулю. Общие уравнения изгиба
пластины:
равен нулю. Общие уравнения изгиба
пластины:
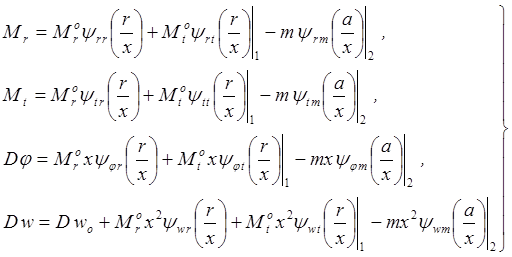 (3.1)
(3.1)
Начальные
параметры ![]() и
и ![]() определяем
из граничных условий:
определяем
из граничных условий:
![]() при
при ![]() ,
(3.2)
,
(3.2)
![]() при
при ![]() .
(3.3)
.
(3.3)
Из условия (3.2) вытекает соотношение:
![]() .
(3.4)
.
(3.4)
Условие (3.3) подставляем в общее уравнение (3.1) для углов поворота нормали:
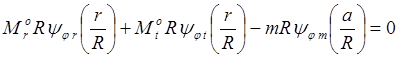 . (3.5)
. (3.5)
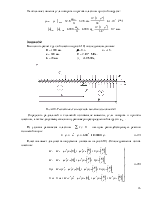
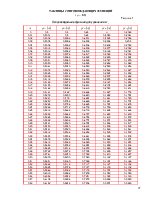
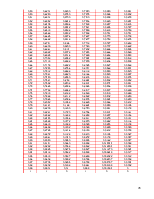
Воспользовавшись
таблицами сопровождающих функций, находим их значения для значений параметра
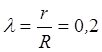 и
и 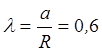 :
:
![]() ,
,
![]() ,
,
![]()
и
подставляем в соотношение (3.5) . Затем из системы уравнений (3.4) и (3.5)
находим неизвестные ![]() ,
, ![]() :
:
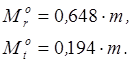
Теперь уравнения (3.1) можно записать в следующем виде:
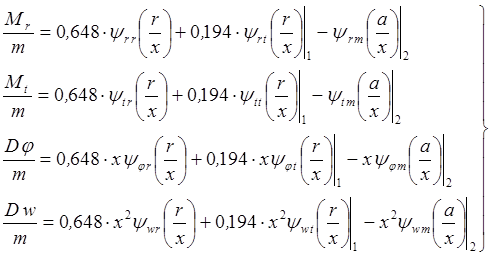 (3.6)
(3.6)
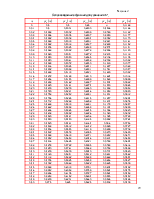
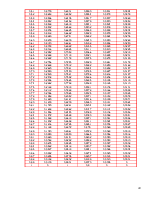
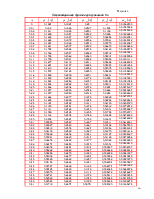
По уравнениям (3.6) производим расчет пластины, задаваясь рядом значений координаты x . Результаты расчета сводим в таблицы 3.1 и 3.2. По полученным результатам строим графики радиальных и кольцевых изгибающих моментов, углов поворота и прогибов пластины (рис.3.2, 3.3, 3.4).
Таблица 3.1
Радиальный и кольцевой изгибающие моменты
|
№ участка |
мм |
|
|
|
|
|
|
|
|
|
|
|
I |
200 308 400 500 571 600-0 |
1 0,65 0,50 0,40 0,35 0,33 |
- |
1 0,7112 0,6250 0,5800 0,5612 0,5545 |
0 0,2888 0,3750 0,4200 0,4388 0,4455 |
- |
0,648 0,517 0,478 0,457 0,449 0,446 |
0 0,2888 0,3750 0,4200 0,4388 0,4455 |
1 0,7112 0,6250 0,5800 0,5612 0,5545 |
- |
0,194 0,325 0,364 0,385 0,393 0,396 |
|
II |
600+0 667 800 1000 |
0,33 0,30 0,25 0,20 |
1 0,90 0,75 0,60 |
0,5545 0,5450 0,5312 0,5200 |
0,4455 0,4550 0,4688 0,4800 |
1 0,9335 0,8469 0,7760 |
-0,554 -0,492 -0,412 -0,346 |
0,4455 0,4550 0,4688 0,4800 |
0,5545 0,5450 0,5312 0,5200 |
0,3 0,3665 0,4531 0,5240 |
0,096 0,034 -0,046 -0,104 |
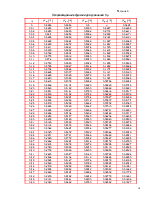
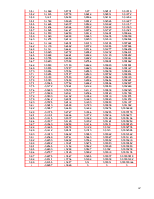
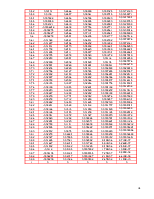
Таблица 3.2
Перемещения точек пластины
|
№ участка |
мм |
|
|
|
|
|
|
|
|
|
|
|
I |
200 308 400 500 571 600-0 |
1 0,65 0,50 0,40 0,35 0,33 |
- |
-0,3297 0,0828 0,2061 0,2704 0,2971 0,3068 |
1,099 0,6865 0,5632 0,4989 0,4722 0,4624 |
- |
0 57,6 97,2 136 162 174 |
0 -0,0190 0,0204 0,0568 0,0769 0,0851 |
0 0,2412 0,2681 0,2663 0,2607 0,2576 |
- |
0 3270 10430 22130 32650 37800 |
|
II |
600+0 667 800 1000 |
0,33 0,30 0,25 0,20 |
1 0,90 0,75 0,60 |
0,3068 0,3204 0,3400 0,3561 |
0,4624 0,4489 0,4293 0,4132 |
0 0,0950 0,2188 0,3200 |
174 133 68 0 |
0,0851 0,0976 0,1185 0,1387 |
0,2576 0,2525 0,2422 0,2307 |
0 0,00483 0,0285 0,0681 |
37800 47730 60980 66530 |
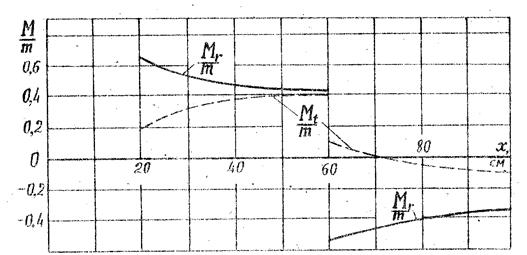
Рис.3.2. Графики радиального и кольцевого изгибающих
моментов в пластине (задача 3.1)
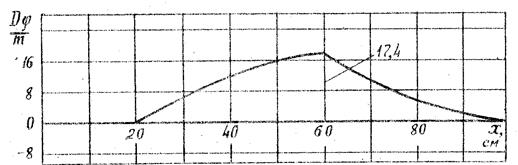
Рис.3.3. График углов поворота нормали к пластине
(задача 3.1)
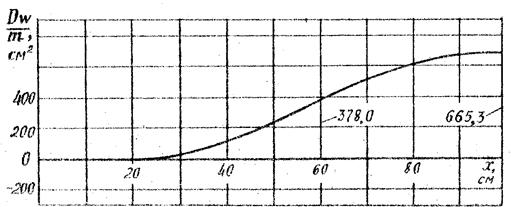
Рис.3.4. График прогибов пластины
(задача 3.1)
Напряженное состояние пластины оцениваем по третьей теории прочности. Проверяем сечения x =200, x = 600-0, x = 600+0. Максимальные эквивалентные напряжения в этих сечениях находим по формулам (0.7) и (0.8):
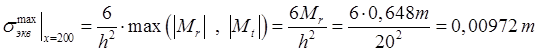 , (3.7)
, (3.7)
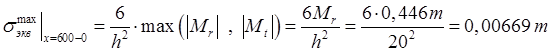 , (3.8)
, (3.8)
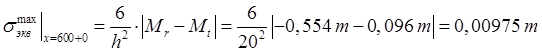 . (3.9)
. (3.9)
Таким образом, наиболее опасным сечением является сечение x = 600+0. Рассмотрим более подробно напряженное состояние в этом сечении. Распределение напряжений по толщине пластины показано на рис.3.5.
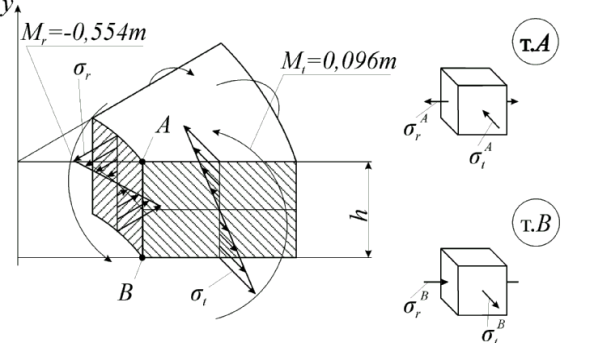
Рис.3.5. Распределение напряжений по толщине пластины
в сечении x = 600+0 (задача 3.1)
Радиальные напряжений на верхнем основании пластины (точка А):
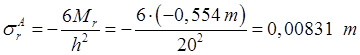 , на
нижнем основании (точка В):
, на
нижнем основании (точка В):
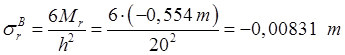 .
.
Кольцевые напряжения:
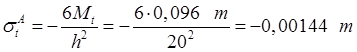 ,
,
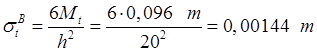 .
.
Нормальные напряжения в площадках, параллельных срединной плоскости пластины, по второй гипотезе Кирхгофа равны нулю.
Схемы напряженного состояния в рассматриваемых точках представлены на рис.3.5.
Эквивалентные напряжения по третьей теории прочности:
![]() ,
,
![]() .
.
Этот результат совпадает с результатом расчета по формуле (3.9).
Условие прочности пластины:
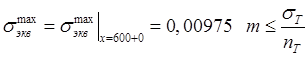 , откуда
допускаемая величина моментной нагрузки:
, откуда
допускаемая величина моментной нагрузки:
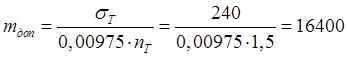 Н×мм/мм.
Н×мм/мм.
Наибольшие значения угла поворота и прогиба пластины при этой величине нагрузки:
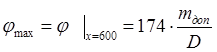 ,
,
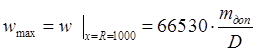 .
.
Цилиндрическая жесткость пластины:
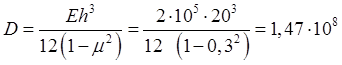 Н×мм.
Н×мм.
Следовательно,
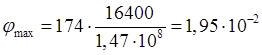 рад,
рад,
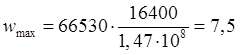 мм.
мм.
Задача 3.2
Выполнить
расчет кольцевой пластины (рис.3.6). Исходные данные для расчета те же, что и в
задаче 3.1. Определить радиальный и кольцевой изгибающие моменты, углы поворота
и прогибы пластины, а также допускаемую величину моментной нагрузки ![]() .
.
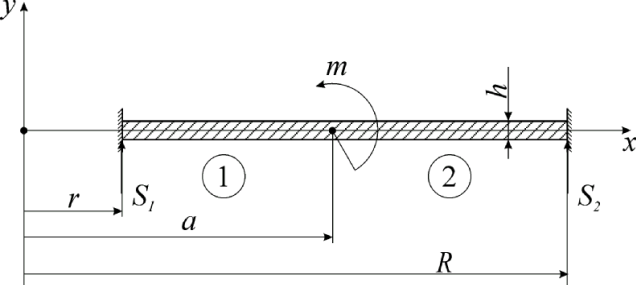
Рис.3.6. Расчетная схема кольцевой пластины (задача 3.2)
В
отличие от пластины, рассмотренной в задаче 3.1, данная пластина является
статически неопределимой. Две вертикальные опорные реакции ![]() и
и ![]() не
могут быть определены из одного уравнения равновесия
не
могут быть определены из одного уравнения равновесия ![]() .
Пластина имеет два участка нагружения (показаны на рис.3.6). Начальный параметр
.
Пластина имеет два участка нагружения (показаны на рис.3.6). Начальный параметр
![]() равен нулю.
равен нулю.
Запишем общие уравнения изгиба пластины:
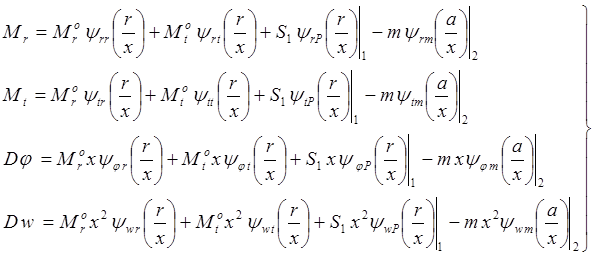 (3.10)
(3.10)
Для определения начальных параметров ![]() ,
, ![]() и
опорных реакций
и
опорных реакций ![]() и
и ![]() используем
граничные условия:
используем
граничные условия:
![]() при
при ![]() ,
(3.11)
,
(3.11)
![]() при
при ![]() , (3.12)
, (3.12)
![]() при
при ![]() (3.13)
(3.13)
и уравнение равновесия пластины:
![]() .
(3.14)
.
(3.14)
Из условия (3.11) следует соотношение:
![]() .
(3.15)
.
(3.15)
Условия (3.12) и (3.13) подставляем в уравнения (3.10) для углов поворота и прогибов пластинки:
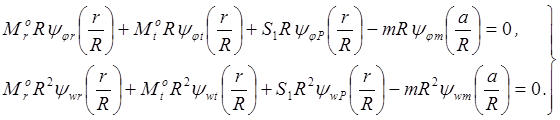 (3.16)
(3.16)
По таблицам находим значения сопровождающих функций:
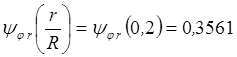 ,
, 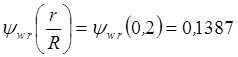 ,
,
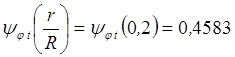 ,
, 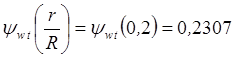 ,
,
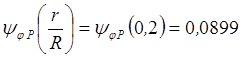 ,
, 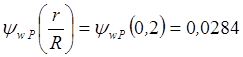 ,
,
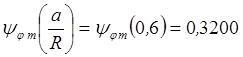 ,
, 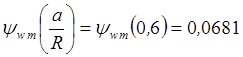 , и подставляем в
уравнения (3.16). Присоединяя к этим уравнениям соотношение (3.15), получаем
систему линейных алгебраических уравнений относительно неизвестных
, и подставляем в
уравнения (3.16). Присоединяя к этим уравнениям соотношение (3.15), получаем
систему линейных алгебраических уравнений относительно неизвестных ![]() :
:
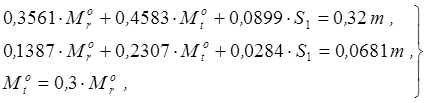 (3.17)
(3.17)
и находим ее решение:
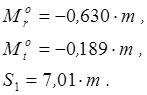
Из уравнения (3.14) теперь можно найти равнодействующую опорной реакции на наружном контуре пластины:
![]() .
.
Подставляя найденные
значения ![]() в уравнения (3.1), получим:
в уравнения (3.1), получим:
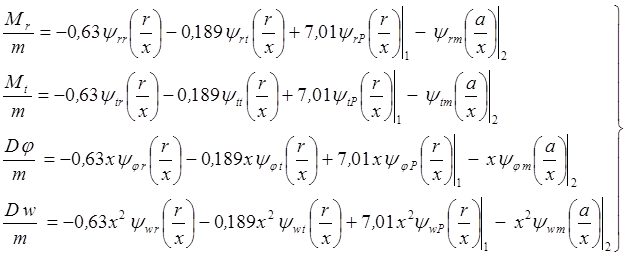 (3.18)
(3.18)
По уравнениям (3.18) выполняем расчет пластины для тех же значений координаты x, что и в задаче 3.1. Значения сопровождающих функций выбираем из таблиц. Результаты расчета сводим в табл.3.3.
Таблица 3.3
Результаты расчета кольцевой пластины
(задача 3.2)
|
№ участка |
мм |
|
|
|
|
|
|
|
I |
200 308 400 500 571 600-0 |
1 0,65 0,50 0,40 0,35 0,33 |
- |
-0,630 -0,077 0,185 0,386 0,497 0,545 |
-0,189 -0,117 0,002 0,125 0,207 0,245 |
0 -31,7 -23,6 5,5 36,5 52,8 |
0 -2250 -5120 -6000 -4430 -2810 |
|
II |
600+0 667 800 1000 |
0,33 0,30 0,25 0,20 |
1 0,90 0,75 0,60 |
-0,455 -0,313 -0,018 0,160 |
-0,055 -0,062 -0,027 0,055 |
52,8 23,3 5,6 0 |
-2810 -890 260 0 |
По результатам расчета строим графики радиального и кольцевого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.