Динамические звенья автоматических систем и их математическое описание. Передаточные функции динамических звеньев. Типовые воздействия, страница 3

№№ варианта	Значение параметров передаточных функций						№№       вари-анта	Значение параметров передаточных функций
						К							К
	с	с	с	с				с	с	с	с
1	1	0,1	0,02	-	-	20	26	0,1	0,02	0,01	-	-	10
2	0,1	0,01	-	-	-	26	27	1	0,02	-	-	-	3
3	0,1	0,01	-	-	-	8	28	0,02	0,002	-	-	-	10
4	0,2	0,02	-	-	-	3	29	0,04	0,1	-	-	-	7
5	1	0,2	0,05	0,01	-	11	30	0,5	0,1	0,01	0,02	-	11
6	0,5	0,05	0,01	-	-	4	31	0,1	0,01	0,005	-	-	15
7	0,2	0,02	-	-	-	7	32	1	0,05	-	-	-	8
8	0,4	0,04	-	-	-	4	33	0,2	0,01	-	-	-	10
9	1	0,1	-	-	0,5/-	5	34	0,1	1	-	-	0,4/-	7
10	0,1	0,01	-	-	0,5/-	6	35	0,005	0,01	-	-	0,4/-	24
11	0,5	0,05	-	-	-	12	36	0,05	0,5	-	-	-	8,5
12	0,8	0,08	-	-	-	2,5	37	0,08	0,8	-	-	-	0,8
13	0,1	0,02	-	-	-	5	38	1	0,01	-	-	-	45
14	0,1	0,01	-	-	0,45/-	1,5	39	0,2	0,02	-	-	0,4/-	3
15	0,05	0,01	-	-	0,75/-	13	40	0,01	0,1	-	-	0,4/-	19
16	0,02	-	-	-	-	30	41	0,04	-	-	-	-	17
17	0,01	0,05	-	-	-	3	42	0,01	0,5	-	-	-	24
18	0,02	-	-	-	-	22	43	0,01	-	-	-	-	40
19	0,3	0,03	0,01	-	-	11	44	0,01	0,02	0,2	-	-	7
20	0,01	-	-	-	-	30	45	0,05	-	-	-	-	7,5
21	0,1	0,02	0,5	-	0,6/-	10	46	0,2	0,02	0,5	-	0,6/-	5
22	0,1	0,01	0,05	-	-	3	47	0,1	0,01	0,05	-	-	8
23	1	0,01	-	-	0,5/0,6	4	48	0,1	0,01	-	-	0,5/0,6	4
24	0,05	0,01	-	-	0,6	3,2	49	0,05	0,01	-	-	0,6	32
25	0,1	0,05	-	-	0,7/-	4	50	0,1	0,005	-	-	0,65/-	7

2.МЕТОДИЧЕСКИЕ УКАЗАНИЯ

2.1 Методические указания к выполнению домашнего                задания 1

Выполнение домашнего задания 1 направлено на усвоение следующих разделов курса;

1)  динамические звенья автоматических систем и их математическое описание;

2)  передаточные функции динамических звеньев;

3)  типовые воздействия;

4)  временные и частотные характеристики динамических звеньев;

            5)  методы построения временных и частотных характеристик динамических звеньев по заданным передаточным функциям.

Переходную h(t) и импульсную переходную функцию w(t) в системах невысокого порядка рекомендуется определять по таблице преобразований Лапласа (см. приложение А), таблица А2, а также по таблицам 8.4-1, 8.4-2, приведенным в (11).

Если известна передаточная функция динамического звена, то

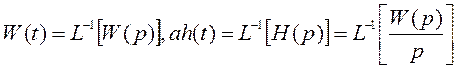
            Для того, чтобы выйти на одно из табличных выражений F(p), необходимо заданную передаточную функцию привести к табличному виду.

            Пусть передаточная функция динамического звена

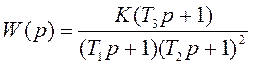                                                                     (2.1)

 тогда                                                                          (2.2)

 В таблице А2 приложения А передаточной функции W(p) соответствует под номером 33 функция

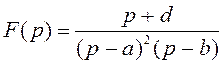                                                                          (2.3)

 Оригинал этой функции

           ,                                                              (2.4)

 где    ;   ;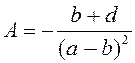  

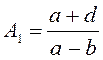 Решение задачи сводится к преобразованию W(p) к виду F(p), которое осуществляется следующим образом :

 

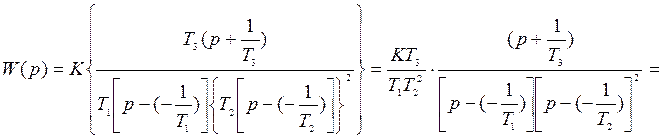
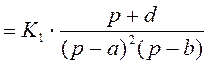   ,                                                                         (2.5)

где  ,   ,  ,  .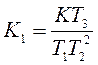

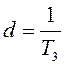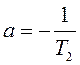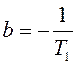Вычислив коэффициенты , d,  a  и  b, находим оригинал 

                                                    (2.6)

 Аналогично определяется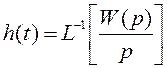   

 Изображению 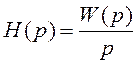 соответствует функция F(p) под номером 37.

Если по таблице преобразований Лапласа не находится изображение, похожее на W(p), то прибегают к разложению W(p) на простые дроби, для которых наверняка есть табличные изображения F(p) в таблице А2.

 Передаточную функцию W(p) можно представить в виде

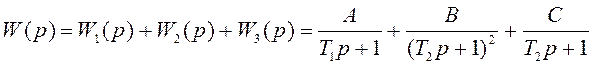      (2.7)

 После приведения W(p) к общему знаменателю получают систему уравнений (2.8)

                                            

                                                            (2.8)                                                                                  

            

 Из системы (2.8) находят коэффициенты А, В, и С. Составляющим , и  передаточной функции W(p) соответствуют в таблице А2 функции F(p) и их оригиналы под номерами соответственно 7, 10 и 7.

            В системах выше третьего порядка, а также в тех случаях, когда возникают  затруднения с переходом от W(p) к табличной функции F(p), можно воспользоваться формулами разложения Хевисайда  /3,С.236-240; 11,С.243-244/.

            Допустим, что динамическое звено (система) автоматического регулирования описывается дифференциальным уравнением вида

 

 

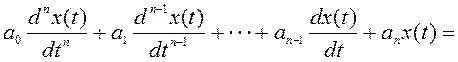
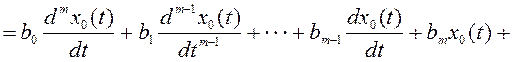
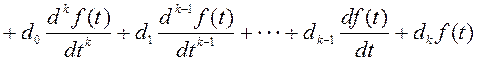                              (2.9)

при начальных условиях ( t = 0)

   ,    ,    … 

            Применив к дифференциальному уравнению (2,9) преобразование Лапласа и учитывая начальные условия, получим вместо (2.9) соответствующее преобразованное алгебраическое уравнение (2.10):

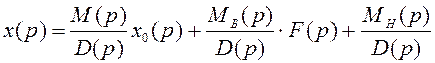  ,                                   (2.10)

где

   ;

   ;

   ;

  

   

            Первое слагаемое уравнения (2.10) определяет движение системы под  действием задающего воздействия при нулевых начальных условиях, второе слагаемое определяет движение системы под действием возмущения при нулевых начальных условиях и третье слагаемое – свободное движение системы под действием начальных условий.

            Если требуется исследовать влияние только начальных условий на поведение системы регулирования, то полагают и  а вместо уравнения (2.10) получают (2.11)

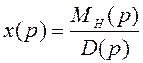                                                                                        (2.11)

              При нулевых начальных условиях и оценке влияния только управляющего воздействия имеют

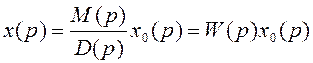                                                           (2.12)