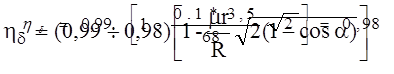 |
Принимая КПД грузового барабана равным КПД блока hгб = 0,98, находим КПД тросовой передачи от лифта к грузовому барабану (без учета потерь в направляющих, которые будут учтены при выборе веса противовеса):
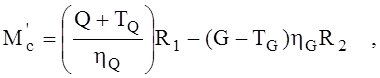 |
Из схемы рис.1 нетрудно усмотреть, что результирующий статический момент, приложенный к грузовому барабану при подъеме лифта,
а результирующий статический момент, приложенный к грузовому барабану при опускании лифта,
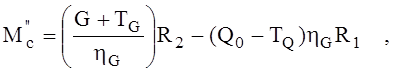 |
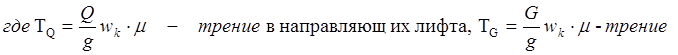 в направлявших
противовеса, g - ускорение свободного падения.
в направлявших
противовеса, g - ускорение свободного падения.
m=0,1 – коэффициент трения
Обозначив wKm/g=e , получим TQ=Qe и TG=Ge . Исходя из принятого условия Mc’=Mc” , имеем
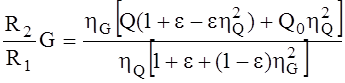 |
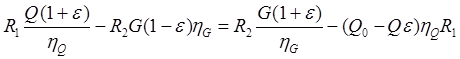
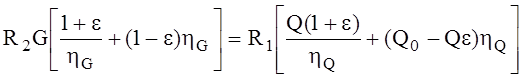 |
Расчёт. Исходя из заданной величины расчетного горизонтального ускорения качки wK находим e :
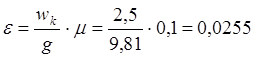 |
По формуле (7) определяем величину (R2G)/R1
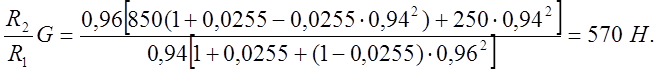 |
Выбор мощности двигателя произведем исходя из наиболее тяжелого для него режима работы-разгона всей системы при подъеме лифта. Для этого изобразим кинематическую схему (рис.З), выделив в ней каждую сосредоточенную массу и заменив отброшенные части привода соответствующими внутренними силами, согласно известному принципу теоретической механики. Задавшись направлением движения, составим уравнения движения каждой выделенной массы.
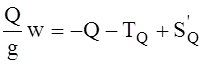 |
|||
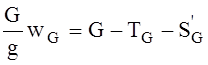 |
|||
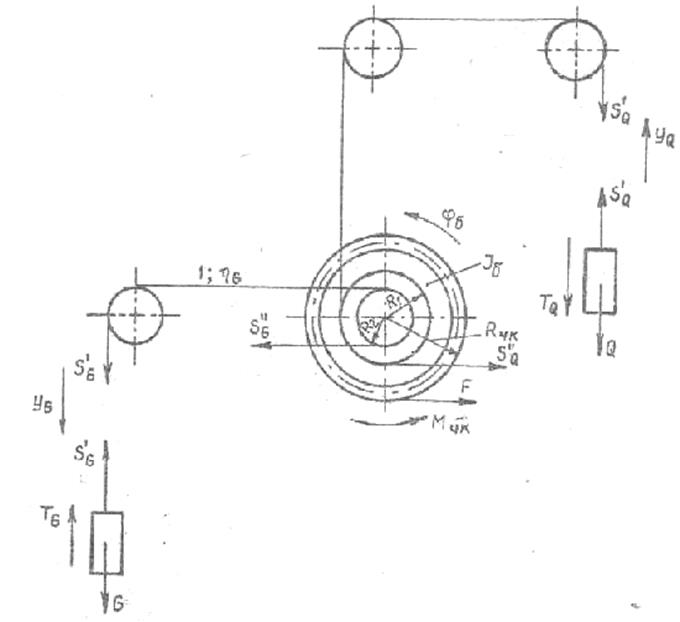 |
Риc.З
где SQ" - усилие, действующее на канат лифта cо стороны грузового барабана, SG" - усилие, дейcтвующее на канат противовеса со стороны грузового барабана, Ri - радиус барабана лифта, R2 - радиус барабана противовеса, jб - угол поворота грузового барабана или что то же барабана противовеса.
Подчеркнем, что в уравнениях (9) и (10) Sq’ и SG’ - это не силы, действующие cо стороны канатов на лифт и противовес, а равные и противоположные им силы, действующие на канаты со стороны лифта и противовеса.
где F- окружная сила, действующая со стороны червяка на червячное колесо, Rчк - радиус червячного колеса, Sq” - усилие, действующее на грузовой барабан со стороны каната лифта. SG” – усилие, действующее на грузовой барабан со стороны каната противовеса.
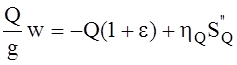 |
|||
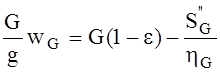 |
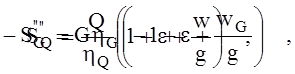 |
|||
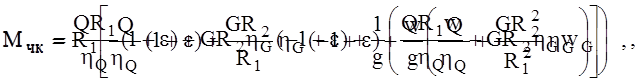 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.